Sampled Traveling Waves
To carry the traveling-wave solution into the ``digital domain,'' it
is necessary to sample the traveling-wave amplitudes at
intervals of ![]() seconds, corresponding to a sampling rate
seconds, corresponding to a sampling rate
![]() samples per second. For CD-quality audio, we have
samples per second. For CD-quality audio, we have
![]() kHz. The natural choice of spatial sampling
interval
kHz. The natural choice of spatial sampling
interval ![]() is the distance sound propagates in one temporal
sampling interval
is the distance sound propagates in one temporal
sampling interval ![]() , or
, or
![]() meters. In a lossless
traveling-wave simulation, the whole wave moves left or right one
spatial sample each time sample; hence, lossless simulation requires
only digital delay lines. By lumping losses parsimoniously in a real
acoustic model, most of the traveling-wave simulation can in fact be
lossless even in a practical application.
meters. In a lossless
traveling-wave simulation, the whole wave moves left or right one
spatial sample each time sample; hence, lossless simulation requires
only digital delay lines. By lumping losses parsimoniously in a real
acoustic model, most of the traveling-wave simulation can in fact be
lossless even in a practical application.
Formally, sampling is carried out by the change of variables
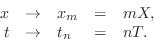
Since
This new notation also introduces a ``
Digital Waveguide Model
![\includegraphics[scale=0.9]{eps/fideal}](http://www.dsprelated.com/josimages_new/pasp/img3287.png) |
In this section, we interpret the sampled d'Alembert traveling-wave solution of the ideal wave equation as a digital filtering framework. This is an example of what are generally known as digital waveguide models [430,431,433,437,442].
The term
![]() in Eq.
in Eq.![]() (C.16) can
be thought of as the output of an
(C.16) can
be thought of as the output of an ![]() -sample delay line whose input is
-sample delay line whose input is
![]() . In general, subtracting a positive number
. In general, subtracting a positive number ![]() from a time
argument
from a time
argument ![]() corresponds to delaying the waveform by
corresponds to delaying the waveform by ![]() samples. Since
samples. Since ![]() is the right-going component, we draw its delay
line with input
is the right-going component, we draw its delay
line with input ![]() on the left and its output
on the left and its output
![]() on the
right. This can be seen as the upper ``rail'' in Fig.C.3
on the
right. This can be seen as the upper ``rail'' in Fig.C.3
Similarly, the term
![]() can be
thought of as the input to an
can be
thought of as the input to an ![]() -sample delay line whose
output is
-sample delay line whose
output is ![]() . Adding
. Adding ![]() to the time argument
to the time argument ![]() produces an
produces an ![]() -sample waveform
advance. Since
-sample waveform
advance. Since ![]() is the left-going component, it makes
sense to draw the delay line with its input
is the left-going component, it makes
sense to draw the delay line with its input
![]() on the right
and its output
on the right
and its output ![]() on the left.
This can be seen as the lower ``rail'' in Fig.C.3.
on the left.
This can be seen as the lower ``rail'' in Fig.C.3.
Note that the position along the string,
![]() meters,
is laid out from left to right in the diagram, giving a physical
interpretation to the horizontal direction in the diagram. Finally,
the left- and right-going traveling waves must be summed to produce a
physical output according to the formula
meters,
is laid out from left to right in the diagram, giving a physical
interpretation to the horizontal direction in the diagram. Finally,
the left- and right-going traveling waves must be summed to produce a
physical output according to the formula
We may compute the physical string displacement at any spatial sampling point
Any ideal, one-dimensional waveguide can be simulated in this way. It
is important to note that the simulation is exact at the
sampling instants, to within the numerical precision of the samples
themselves. To avoid aliasing associated with sampling, we
require all waveshapes traveling along the string to be initially
bandlimited to less than half the sampling frequency. In other
words, the highest frequencies present in the signals ![]() and
and
![]() may not exceed half the temporal sampling frequency
may not exceed half the temporal sampling frequency
![]() ; equivalently, the highest spatial
frequencies in the shapes
; equivalently, the highest spatial
frequencies in the shapes ![]() and
and ![]() may not exceed
half the spatial sampling frequency
may not exceed
half the spatial sampling frequency
![]() .
.
A C program implementing a plucked/struck string model in the form of Fig.C.3 is available at http://ccrma.stanford.edu/~jos/pmudw/.
Digital Waveguide Interpolation
A more compact simulation diagram which stands for either sampled or
continuous waveguide simulation is shown in Fig.C.4.
The figure emphasizes that the ideal, lossless waveguide is simulated
by a bidirectional delay line, and that bandlimited
spatial interpolation may be used to construct a displacement
output for an arbitrary ![]() not a multiple of
not a multiple of ![]() , as suggested by
the output drawn in Fig.C.4. Similarly, bandlimited
interpolation across time serves to evaluate the waveform at an
arbitrary time not an integer multiple of
, as suggested by
the output drawn in Fig.C.4. Similarly, bandlimited
interpolation across time serves to evaluate the waveform at an
arbitrary time not an integer multiple of ![]() (§4.4).
(§4.4).
Ideally, bandlimited interpolation is carried out by convolving a
continuous ``sinc function''
sinc![]() with the signal samples. Specifically, convolving a sampled signal
with the signal samples. Specifically, convolving a sampled signal
![]() with
sinc
with
sinc![]() ``evaluates'' the signal at an
arbitrary continuous time
``evaluates'' the signal at an
arbitrary continuous time ![]() . The sinc function is the impulse
response of the ideal lowpass filter which cuts off at half the
sampling rate.
. The sinc function is the impulse
response of the ideal lowpass filter which cuts off at half the
sampling rate.
In practice, the interpolating sinc function must be windowed
to a finite duration. This means the associated lowpass filter must
be granted a ``transition band'' in which its frequency response is
allowed to ``roll off'' to zero at half the sampling rate. The
interpolation quality in the ``pass band'' can always be made perfect
to within the resolution of human hearing by choosing a sufficiently
large product of window-length times transition-bandwidth. Given
``audibly perfect'' quality in the pass band, increasing the
transition bandwidth reduces the computational expense of the
interpolation. In fact, they are approximately inversely
proportional. This is one reason why oversampling at rates
higher than twice the highest audio frequency is helpful. For
example, at a ![]() kHz sampling rate, the transition bandwidth above
the nominal audio upper limit of
kHz sampling rate, the transition bandwidth above
the nominal audio upper limit of ![]() kHz is only
kHz is only ![]() kHz, while at
a
kHz, while at
a ![]() kHz sampling rate (used in DAT machines) the guard band is
kHz sampling rate (used in DAT machines) the guard band is ![]() kHz wide--nearly double. Since the required window length (impulse
response duration) varies inversely with the provided transition
bandwidth, we see that increasing the sampling rate by less than ten
percent reduces the filter expense by almost fifty percent.
Windowed-sinc interpolation is described further in
§4.4. Many more techniques for digital resampling
and delay-line interpolation are reviewed in
[267].
kHz wide--nearly double. Since the required window length (impulse
response duration) varies inversely with the provided transition
bandwidth, we see that increasing the sampling rate by less than ten
percent reduces the filter expense by almost fifty percent.
Windowed-sinc interpolation is described further in
§4.4. Many more techniques for digital resampling
and delay-line interpolation are reviewed in
[267].
Relation to the Finite Difference Recursion
In this section we will show that the digital waveguide simulation technique is equivalent to the recursion produced by the finite difference approximation (FDA) applied to the wave equation [442, pp. 430-431]. A more detailed derivation, with examples and exploration of implications, appears in Appendix E. Recall from (C.6) that the time update recursion for the ideal string digitized via the FDA is given by
| (C.18) |
To compare this with the waveguide description, we substitute the traveling-wave decomposition
| (C.19) | |||
Thus, we obtain the result that the FDA recursion is also exact in the lossless case, because it is equivalent to the digital waveguide method which we know is exact at the sampling points. This is surprising since the FDA introduces artificial damping when applied to lumped, mass-spring systems, as discussed earlier.
The last identity above can be rewritten as
| (C.20) | |||
which says the displacement at time
This results extends readily to the digital waveguide mesh (§C.14), which is essentially a lattice-work of digital waveguides for simulating membranes and volumes. The equivalence is important in higher dimensions because the finite-difference model requires less computations per node than the digital waveguide approach.
Even in one dimension, the digital waveguide and finite-difference
methods have unique advantages in particular situations, and as a
result they are often combined together to form a hybrid
traveling-wave/physical-variable simulation
[351,352,222,124,123,224,263,223].
In this hybrid simulations, the traveling-wave variables are called
``W variables'' (where `W' stands for ``Wave''), while the physical
variables are caled ``K variables'' (where `K' stands for
``Kirchoff''). Each K variable, such as displacement ![]() on a vibrating string, can be regarded as the sum of two
traveling-wave components, or W variables:
on a vibrating string, can be regarded as the sum of two
traveling-wave components, or W variables:
Next Section:
A Lossy 1D Wave Equation
Previous Section:
Traveling-Wave Solution








![\includegraphics[scale=0.9]{eps/fcompact}](http://www.dsprelated.com/josimages_new/pasp/img3301.png)











