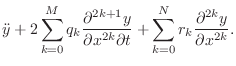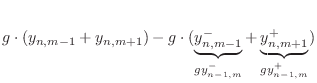Free Books    Physical Audio Signal Processing  

A Lossy 1D Wave Equation

In any real vibrating string, there are energy losses due to yielding terminations, drag by the surrounding air, and internal friction within the string. While losses in solids generally vary in a complicated way with frequency, they can usually be well approximated by a small number of odd-order terms added to the wave equation. In the simplest case, force is directly proportional to transverse string velocity, independent of frequency. If this proportionality constant is $ \mu $, we obtain the modified wave equation

$\displaystyle Ky''= \epsilon {\ddot y}+ \mu{\dot y}.$ (C.21)

Thus, the wave equation has been extended by a ``first-order'' term, i.e., a term proportional to the first derivative of $ y$ with respect to time. More realistic loss approximations would append terms proportional to $ {\dddot y}$, $ {\partial^5 y/\partial t^5}$, and so on, giving frequency-dependent losses.

Setting $ y(t,x) = e^{st+vx}$ in the wave equation to find the relationship between temporal and spatial frequencies in the eigensolution, the wave equation becomes

$\displaystyle K\left(v^2 y\right)$ $\displaystyle =$ $\displaystyle \epsilon \left(s^2 y\right)+ \mu\left(s y\right) \,\,\Rightarrow\,\,Kv^2 = \epsilon s^2 + \mu s$  
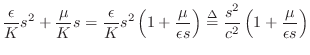$\displaystyle \,\,\Rightarrow\,\,v^2$ $\displaystyle =$ $\displaystyle \frac{\epsilon }{K} s^2 + \frac{\mu}{K} s = \frac{\epsilon }{K} s... ...on s}} \right) \isdef \frac{s^2}{c^2}\left(1 + {\frac{\mu}{\epsilon s}} \right)$  
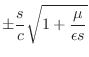$\displaystyle \,\,\Rightarrow\,\,v$ $\displaystyle =$ $\displaystyle \pm \frac{s}{c} \sqrt{1 + {\frac{\mu}{\epsilon s}}}$  

where $ c \isdef \sqrt{K/\epsilon }$ is the wave velocity in the lossless case. At high frequencies (large $ \vert s\vert$), or when the friction coefficient $ \mu $ is small relative to the mass density $ \epsilon $ at the lowest frequency of interest, we have the approximation

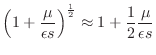$\displaystyle \left(1 + {\frac{\mu}{\epsilon s}}\right)^\frac{1}{2} \approx 1 + \frac{1}{2}{\frac{\mu}{\epsilon s}}$ (C.22)

by the binomial theorem. For this small-loss approximation, we obtain the following relationship between temporal and spatial frequency:

$\displaystyle v \approx \pm \frac{1}{c}\left({s + \frac{\mu}{2\epsilon }} \right)$ (C.23)

The eigensolution is then

$\displaystyle e^{st+vx} = \exp{\left[st\pm \left({s + \frac{\mu}{2\epsilon }}\r... ...c{x}{c}\right)\right]} \exp{\left(\pm\frac{\mu}{2\epsilon }\frac{x}{c}\right)}.$ (C.24)

The right-going part of the eigensolution is

$\displaystyle e^{-{\left(\mu/2\epsilon \right)}{x/c}} e^{s \left(t - {x/c}\right)}$ (C.25)

which decays exponentially in the direction of propagation, and the left-going solution is

$\displaystyle e^{{\left(\mu/2\epsilon \right)}{x/c}} e^{s \left(t + {x/c}\right)}$ (C.26)

which also decays exponentially in the direction of travel.

Setting $ s=j\omega$ and using superposition to build up arbitrary traveling wave shapes, we obtain the general class of solutions

$\displaystyle y(t,x) = e^{-{\left(\mu/2\epsilon \right)}{x/c}} y_r\left(t-{x/c}\right) + e^{{\left(\mu/2\epsilon \right)}{x/c}} y_l\left(t+{x/c}\right).$ (C.27)

Sampling these exponentially decaying traveling waves at intervals of $ T$ seconds (or $ X=cT$ meters) gives

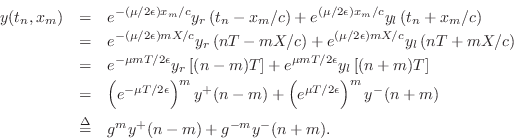
\begin{eqnarray*} y(t_n,x_m) &=& e^{-{\left(\mu/2\epsilon \right)}{x_m/c}} y_r\l... ... y^{-}(n+m) \\ &\isdef & g^{m} y^{+}(n-m) + g^{-m} y^{-}(n+m). \end{eqnarray*}

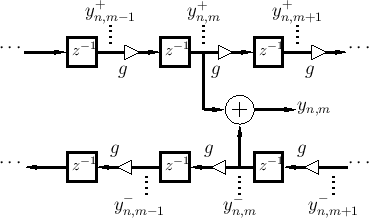
The simulation diagram for the lossy digital waveguide is shown in Fig.C.5.

Figure C.5: Discrete simulation of the ideal, lossy waveguide.
\includegraphics[scale=0.9]{eps/floss}

Again the discrete-time simulation of the decaying traveling-wave solution is an exact implementation of the continuous-time solution at the sampling positions and instants, even though losses are admitted in the wave equation. Note also that the losses which are distributed in the continuous solution have been consolidated, or lumped, at discrete intervals of $ cT$ meters in the simulation. The loss factor $ g = e^{-{\mu T/2\epsilon }}$ summarizes the distributed loss incurred in one sampling interval. The lumping of distributed losses does not introduce an approximation error at the sampling points. Furthermore, bandlimited interpolation can yield arbitrarily accurate reconstruction between samples. The only restriction is again that all initial conditions and excitations be bandlimited to below half the sampling rate.

Loss Consolidation

In many applications, it is possible to realize vast computational savings in digital waveguide models by commuting losses out of unobserved and undriven sections of the medium and consolidating them at a minimum number of points. Because the digital simulation is linear and time invariant (given constant medium parameters $ K,\epsilon ,\mu$), and because linear, time-invariant elements commute, the diagram in Fig.C.6 is exactly equivalent (to within numerical precision) to the previous diagram in Fig.C.5.

Figure C.6: Discrete simulation of the ideal, lossy waveguide. Each per-sample loss factor $ g$ may be ``pushed through'' delay elements and combined with other loss factors until an input or output is encountered which inhibits further migration. If further consolidation is possible on the other side of a branching node, a loss factor can be pushed through the node by pushing a copy into each departing branch. If there are other inputs to the node, the inverse of the loss factor must appear on each of them. Similar remarks apply to pushing backwards through a node.
\includegraphics[scale=0.9]{eps/flloss}

Frequency-Dependent Losses

In nearly all natural wave phenomena, losses increase with frequency. Distributed losses due to air drag and internal bulk losses in the string tend to increase monotonically with frequency. Similarly, air absorption increases with frequency, adding loss for sound waves in acoustic tubes or open air [318].

Perhaps the apparently simplest modification to Eq.$ \,$(C.21) yielding frequency-dependent damping is to add a third-order time-derivative term [392]:

$\displaystyle Ky''= \epsilon {\ddot y}+ \mu{\dot y}+ \mu_3{\dddot y} \protect$ (C.28)

While this model has been successful in practice [77], it turns out to go unstable at very high sampling rates. The technical term for this problem is that the PDE is ill posed [45].

A well posed replacement for Eq.$ \,$(C.28) is given by

$\displaystyle Ky''= \epsilon {\ddot y}+ \mu{\dot y}+ \mu_2{\dot y''} \protect$ (C.29)

in which the third-order partial derivative with respect to time, $ {\dddot y}$, has been replaced by a third-order mixed partial derivative--twice with respect to $ x$ and once with respect to $ t$.

The solution of a lossy wave equation containing higher odd-order derivatives with respect to time yields traveling waves which propagate with frequency-dependent attenuation. Instead of scalar factors $ g$ distributed throughout the diagram as in Fig.C.5, each $ g$ factor becomes a lowpass filter having some frequency-response per sample denoted by $ G(\omega)$. Because propagation is passive, we will always have $ \left\vert G(\omega)\right\vert\leq 1$.

More specically, As shown in [392], odd-order partial derivatives with respect to time in the wave equation of the form

$\displaystyle \frac{\partial^n}{\partial t^n} y(t,x), \quad n=1,3,5,\ldots, $

correspond to attenuation of traveling waves on the string. (The even-order time derivatives can be associated with variations in dispersion as a function of frequency, which is considered in §C.6 below.) For $ n>1$, the losses are frequency dependent, and the per-sample amplitude-response ``rolls off'' proportional to

$\displaystyle G(\omega) \propto \frac{1}{\omega^{n-1}},$   $\displaystyle \mbox{($n$\ odd)}$$\displaystyle . $

In particular, if the wave equation (C.21) is modified by adding terms proportional to $ \mu_3{\dddot y}$ and $ \mu_5{\partial^5 y/\partial t^5}$, for instance, then the per-sample propagation gain $ G(\omega)$ has the form

$\displaystyle G(\omega) = g_0 + g_2 \omega^2 + g_4 \omega^4 $

where the $ g_i$ are constants depending on the constants $ \mu_3$ and $ \mu_5$ in the wave equation. Since these per-sample loss filters are linear and time-invariant [449], they may also be consolidated at a minimum number of points in the waveguide without introducing any approximation error, just like the constant gains $ g$ in Fig.C.5. This result does not extend precisely to the waveguide mesh (§C.14).

In view of the above, we see that we can add odd-order time derivatives to the wave equation to approximate experimentally observed frequency-dependent damping characteristics in vibrating strings [73]. However, we then have the problem that such wave equations are ill posed, leading to possible stability failures at high sampling rates. As a result, it is generally preferable to use mixed derivatives, as in Eq.$ \,$(C.29), and try to achieve realistic damping using higher order spatial derivatives instead.

Well Posed PDEs for Modeling Damped Strings

A large class of well posed PDEs is given by [45]

$\displaystyle {\ddot y} + 2\sum_{k=0}^M q_k \frac{\partial^{2k+1}y}{\partial x^{2k}\partial t} + \sum_{k=0}^N r_k\frac{\partial^{2k}y}{\partial x^{2k}}. \protect$ (C.30)

Thus, to the ideal string wave equation Eq.$ \,$(C.1) we add any number of even-order partial derivatives in $ x$, plus any number of mixed odd-order partial derivatives in $ x$ and $ t$, where differentiation with respect to $ t$ occurs only once. Because every member of this class of PDEs is only second-order in time, it is guaranteed to be well posed, as shown in §D.2.2.

Digital Filter Models of Damped Strings

In an efficient digital simulation, lumped loss factors of the form $ G^k(\omega)$ are approximated by a rational frequency response $ {\hat G}_k(e^{j\omega T})$. In general, the coefficients of the optimal rational loss filter are obtained by minimizing $ \vert\vert\,G^k(\omega) - {\hat G}_k(e^{j\omega T})\,\vert\vert $ with respect to the filter coefficients or the poles and zeros of the filter. To avoid introducing frequency-dependent delay, the loss filter should be a zero-phase, finite-impulse-response (FIR) filter [362]. Restriction to zero phase requires the impulse response $ {\hat g}_k(n)$ to be finite in length (i.e., an FIR filter) and it must be symmetric about time zero, i.e., $ {\hat g}_k(-n)={\hat g}_k(n)$. In most implementations, the zero-phase FIR filter can be converted into a causal, linear phase filter by reducing an adjacent delay line by half of the impulse-response duration.

Lossy Finite Difference Recursion

We will now derive a finite-difference model in terms of string displacement samples which correspond to the lossy digital waveguide model of Fig.C.5. This derivation generalizes the lossless case considered in §C.4.3.

Figure C.7 depicts a digital waveguide section once again in ``physical canonical form,'' as shown earlier in Fig.C.5, and introduces a doubly indexed notation for greater clarity in the derivation below [442,222,124,123].

Figure C.7: Lossy digital waveguide--frequency-independent loss-factors $ g$.
\includegraphics{eps/wglossy}

Referring to Fig.C.7, we have the following time-update relations:

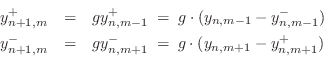
\begin{eqnarray*} y^{+}_{n+1,m}&=& gy^{+}_{n,m-1}\;=\; g\cdot(y_{n,m-1}- y^{-}_{... ..._{n+1,m}&=& gy^{-}_{n,m+1}\;=\; g\cdot(y_{n,m+1}- y^{+}_{n,m+1}) \end{eqnarray*}

Adding these equations gives

$\displaystyle y_{n+1,m}$ $\displaystyle =$ $\displaystyle g\cdot(y_{n,m-1}+y_{n,m+1}) - g\cdot(\underbrace{y^{-}_{n,m-1}}_{gy^{-}_{n-1,m}} + \underbrace{y^{+}_{n,m+1}}_{gy^{+}_{n-1,m}})$  
  $\displaystyle =$ $\displaystyle g\cdot(y_{n,m-1}+y_{n,m+1}) - g^2 y_{n-1,m} \protect$ (C.31)

This is now in the form of the finite-difference time-domain (FDTD) scheme analyzed in [222]:

$\displaystyle y_{n+1,m}= g^{+}_my_{n,m-1}+ g^{-}_my_{n,m+1}+ a_my_{n-1,m}, $

with $ g^{+}_m= g^{-}_m= g$, and $ a_m= -g^2$. In [124], it was shown by von Neumann analysis (§D.4) that these parameter choices give rise to a stable finite-difference scheme (§D.2.3), provided $ \vert g\vert\leq 1$. In the present context, we expect stability to follow naturally from starting with a passive digital waveguide model.

Frequency-Dependent Losses

The preceding derivation generalizes immediately to frequency-dependent losses. First imagine each $ g$ in Fig.C.7 to be replaced by $ G(z)$, where for passivity we require

$\displaystyle \left\vert G(e^{j\omega T})\right\vert\leq 1. $

In the time domain, we interpret $ g(n)$ as the impulse response corresponding to $ G(z)$. We may now derive the frequency-dependent counterpart of Eq.$ \,$(C.31) as follows:

\begin{eqnarray*} y^{+}_{n+1,m}&=& g\ast y^{+}_{n,m-1}\;=\; g\ast (y_{n,m-1}- y^... ... &=& g\ast \left[(y_{n,m-1}+y_{n,m+1}) - g\ast y_{n-1,m}\right] \end{eqnarray*}

where $ \ast $ denotes convolution (in the time dimension only). Define filtered node variables by

\begin{eqnarray*} y^f_{n,m}&=& g\ast y_{n,m}\\ y^{ff}_{n,m}&=& g\ast y^f_{n,m}. \end{eqnarray*}

Then the frequency-dependent FDTD scheme is simply

$\displaystyle y_{n+1,m}= y^f_{n,m-1}+ y^f_{n,m+1}- y^{ff}_{n-1,m}. $

We see that generalizing the FDTD scheme to frequency-dependent losses requires a simple filtering of each node variable $ y_{n,m}$ by the per-sample propagation filter $ G(z)$. For computational efficiency, two spatial lines should be stored in memory at time $ n$: $ y^f_{n,m}$ and $ y^{ff}_{n-1,m}$, for all $ m$. These state variables enable computation of $ y_{n+1,m}$, after which each sample of $ y^f_{n,m}$ ($ \forall m$) is filtered by $ G(z)$ to produce $ y^{ff}_{n-1,m}$ for the next iteration, and $ y_{n+1,m}$ is filtered by $ G(z)$ to produce $ y^f_{n,m}$ for the next iteration.

The frequency-dependent generalization of the FDTD scheme described in this section extends readily to the digital waveguide mesh. See §C.14.5 for the outline of the derivation.

Next Section:
The Dispersive 1D Wave Equation
Previous Section:
Sampled Traveling Waves