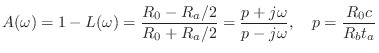Tonehole Modeling
Toneholes in woodwind instruments are essentially cylindrical holes in
the bore. One modeling approach would be to treat the tonehole as a
small waveguide which connects to the main bore via one port on a
three-port junction. However, since the tonehole length is small
compared with the distance sound travels in one sampling instant (
![]() in, e.g.), it is more straightforward to treat the
tonehole as a lumped load along the bore, and most modeling efforts
have taken this approach.
in, e.g.), it is more straightforward to treat the
tonehole as a lumped load along the bore, and most modeling efforts
have taken this approach.
The musical acoustics literature contains experimentally verified models of tone-hole acoustics, such as by Keefe [238]. Keefe's tonehole model is formulated as a ``transmission matrix'' description, which we may convert to a traveling-wave formulation by a simple linear transformation (described in §9.5.4 below) [465]. For typical fingerings, the first few open tone holes jointly provide a bore termination [38]. Either the individual tone holes can be modeled as (interpolated) scattering junctions, or the whole ensemble of terminating tone holes can be modeled in aggregate using a single reflection and transmission filter, like the bell model. Since the tone hole diameters are small compared with most audio frequency wavelengths, the reflection and transmission coefficients can be implemented to a reasonable approximation as constants, as opposed to cross-over filters as in the bell. Taking into account the inertance of the air mass in the tone hole, the tone hole can be modeled as a two-port loaded junction having load impedance equal to the air-mass inertance [143,509]. At a higher level of accuracy, adapting transmission-matrix parameters from the existing musical acoustics literature leads to first-order reflection and transmission filters [238,406,403,404,465]. The individual tone-hole models can be simple lossy two-port junctions, modeling only the internal bore loss characteristics, or three-port junctions, modeling also the transmission characteristics to the outside air. Another approach to modeling toneholes is the ``wave digital'' model [527] (see §F.1 for a tutorial introduction to this approach). The subject of tone-hole modeling is elaborated further in [406,502]. For simplest practical implementation, the bell model can be used unchanged for all tunings, as if the bore were being cut to a new length for each note and the same bell were attached. However, for best results in dynamic performance, the tonehole model should additionally include an explicit valve model for physically accurate behavior when slowly opening or closing the tonehole [405].
The Clarinet Tonehole as a Two-Port Junction
The clarinet tonehole model developed by Keefe [240] is
parametrized in terms of series and shunt resistance and reactance, as
shown in Fig. 9.43. The transmission
matrix description of this two-port is given by the product of the
transmission matrices for the series impedance ![]() , shunt
impedance
, shunt
impedance ![]() , and series impedance
, and series impedance ![]() , respectively:
, respectively:
where all quantities are written in the frequency domain, and the impedance parameters are given by
| (open-hole shunt impedance) |
|||
| (closed-hole shunt impedance) |
(10.51) | ||
| (open-hole series impedance) |
|||
| (closed-hole series impedance) |
where
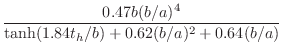 |
|||
 |
where
![$\displaystyle t_h = t_w + \frac{1}{8}\frac{b^2}{a}\left[1+0.172\left(\frac{b}{a}\right)^2\right]
$](http://www.dsprelated.com/josimages_new/pasp/img2426.png)
Note that the specific resistance of the open tonehole, ![]() , is the
only real impedance and therefore the only source of wave energy loss at
the tonehole. It is given by [240]
, is the
only real impedance and therefore the only source of wave energy loss at
the tonehole. It is given by [240]
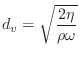
![$\displaystyle \alpha = \frac{1}{2bc}\left[\,\sqrt{\frac{2\eta\omega}{\rho}}
+ (\gamma-1)\sqrt{\frac{2\kappa\omega}{\rho C_p}}\,\right]
$](http://www.dsprelated.com/josimages_new/pasp/img2433.png)
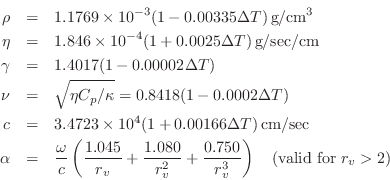
where
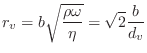
The open-hole effective length ![]() , assuming no pad above the hole,
is given in
[240] as
, assuming no pad above the hole,
is given in
[240] as
![$\displaystyle t_e = \frac{(1/k)\tan(kt) + b [1.40 - 0.58(b/a)^2]}{1 - 0.61 kb \tan(kt)}
$](http://www.dsprelated.com/josimages_new/pasp/img2445.png)
For implementation in a digital waveguide model, the lumped parameters above must be converted to scattering parameters. Such formulations of toneholes have appeared in the literature: Vesa Välimäki [509,502] developed tonehole models based on a ``three-port'' digital waveguide junction loaded by an inertance, as described in Fletcher and Rossing [143], and also extended his results to the case of interpolated digital waveguides. It should be noted in this context, however, that in the terminology of Appendix C, Välimäki's tonehole representation is a loaded 2-port junction rather than a three-port junction. (A load can be considered formally equivalent to a ``waveguide'' having wave impedance given by the load impedance.) Scavone and Smith [402] developed digital waveguide tonehole models based on the more rigorous ``symmetric T'' acoustic model of Keefe [240], using general purpose digital filter design techniques to obtain rational approximations to the ideal tonehole frequency response. A detailed treatment appears in Scavone's CCRMA Ph.D. thesis [406]. This section, adapted from [465], considers an exact translation of the Keefe tonehole model, obtaining two one-filter implementations: the ``shared reflectance'' and ``shared transmittance'' forms. These forms are shown to be stable without introducing an approximation which neglects the series inertance terms in the tonehole model.
By substituting
![]() in (9.53) to convert spatial
frequency to temporal frequency, and by substituting
in (9.53) to convert spatial
frequency to temporal frequency, and by substituting
| (10.52) | |||
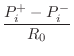 |
(10.53) |
for
Clear["t*", "p*", "u*", "r*"]
transmissionMatrix = {{t11, t12}, {t21, t22}};
leftPort = {{p2p+p2m}, {(p2p-p2m)/r2}};
rightPort = {{p1p+p1m}, {(p1p-p1m)/r1}};
Format[t11, TeXForm] := "{T_{11}}"
Format[p1p, TeXForm] := "{P_1^+}"
... (etc. for all variables) ...
TeXForm[Simplify[Solve[leftPort ==
transmissionMatrix . rightPort, {p1m, p2p}]]]
The above code produces the following formulas:
Substituting relevant values for Keefe's tonehole model, we obtain, in matrix notation,
We thus obtain the scattering formulation depicted in Fig. 9.44, where
is the reflectance of the tonehole (the same from either direction), and
is the transmittance of the tonehole (also the same from either direction). The notation ``
The approximate forms in (9.57) and (9.58) are obtained by neglecting
the negative series inertance ![]() which serves to adjust the effective
length of the bore, and which therefore can be implemented elsewhere in the
interpolated delay-line calculation as discussed further below. The open
and closed tonehole cases are obtained by substituting
which serves to adjust the effective
length of the bore, and which therefore can be implemented elsewhere in the
interpolated delay-line calculation as discussed further below. The open
and closed tonehole cases are obtained by substituting
![]() and
and
![]() , respectively, from (9.53).
, respectively, from (9.53).
In a manner analogous to converting the four-multiply Kelly-Lochbaum (KL)
scattering junction
[245]
into a one-multiply form (cf. (C.60) and
(C.62) on page ![]() ), we may pursue a ``one-filter'' form of the waveguide
tonehole model. However, the series inertance gives some initial trouble,
since
), we may pursue a ``one-filter'' form of the waveguide
tonehole model. However, the series inertance gives some initial trouble,
since
![$\displaystyle [1+S(\omega)] - T(\omega) = \frac{2R_a}{2R_0+ R_a} \isdef L(\omega)
$](http://www.dsprelated.com/josimages_new/pasp/img2469.png)
| (10.58) |
and, similarly,
| (10.59) |
The resulting tonehole implementation is shown in Fig. 9.45. We call this the ``shared reflectance'' form of the tonehole junction.
In the same way, an alternate form is obtained from the substitution
| (10.60) | |||
| (10.61) |
shown in Fig. 9.46.
![\includegraphics[scale=0.9]{eps/fFingerHoleOneMulCommuted}](http://www.dsprelated.com/josimages_new/pasp/img2487.png) |
Since
![]() , it can be neglected to first order, and
, it can be neglected to first order, and
![]() , reducing both of the above forms to an approximate
``one-filter'' tonehole implementation.
, reducing both of the above forms to an approximate
``one-filter'' tonehole implementation.
Since
![]() is a pure negative reactance, we have
is a pure negative reactance, we have
In this form, it is clear that
We now see precisely how the negative series inertance ![]() provides a
negative, frequency-dependent, length correction for the bore. From
(9.63),
the phase delay of
provides a
negative, frequency-dependent, length correction for the bore. From
(9.63),
the phase delay of ![]() can be computed as
can be computed as
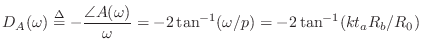
In practice, it is common to combine all delay corrections into a single ``tuning allpass filter'' for the whole bore [428,207]. Whenever the desired allpass delay goes negative, we simply add a sample of delay to the desired allpass phase-delay and subtract it from the nearest delay. In other words, negative delays have to be ``pulled out'' of the allpass and used to shorten an adjacent interpolated delay line. Such delay lines are normally available in practical modeling situations.
Tonehole Filter Design
The tone-hole reflectance and transmittance must be converted to
discrete-time form for implementation in a digital waveguide model.
Figure 9.49 plots the responses of second-order discrete-time
filters designed to approximate the continuous-time magnitude and phase
characteristics of the reflectances for closed and open toneholes, as
carried out in [403,406]. These filter designs
assumed a tonehole of radius ![]() mm, minimum tonehole height
mm, minimum tonehole height
![]() mm, tonehole radius of curvature
mm, tonehole radius of curvature
![]() mm, and air column
radius
mm, and air column
radius ![]() mm. Since the measurements of Keefe do not extend to 5
kHz, the continuous-time responses in the figures are extrapolated above
this limit. Correspondingly, the filter designs were weighted to produce
best results below 5 kHz.
mm. Since the measurements of Keefe do not extend to 5
kHz, the continuous-time responses in the figures are extrapolated above
this limit. Correspondingly, the filter designs were weighted to produce
best results below 5 kHz.
The closed-hole filter design was carried out using weighted ![]() equation-error minimization [428, p. 47], i.e., by minimizing
equation-error minimization [428, p. 47], i.e., by minimizing
![]() , where
, where ![]() is the weighting
function,
is the weighting
function,
![]() is the desired frequency response,
is the desired frequency response, ![]() denotes
discrete-time radian frequency, and the designed filter response is
denotes
discrete-time radian frequency, and the designed filter response is
![]() . Note that both phase and magnitude are
matched by equation-error minimization, and this error criterion is used
extensively in the field of system identification [288]
due to its ability to design optimal IIR filters via quadratic
minimization. In the spirit of the well-known Steiglitz-McBride algorithm
[287], equation-error minimization can be iterated,
setting the weighting function at iteration
. Note that both phase and magnitude are
matched by equation-error minimization, and this error criterion is used
extensively in the field of system identification [288]
due to its ability to design optimal IIR filters via quadratic
minimization. In the spirit of the well-known Steiglitz-McBride algorithm
[287], equation-error minimization can be iterated,
setting the weighting function at iteration ![]() to the inverse of the
inherent weighting
to the inverse of the
inherent weighting
![]() of the previous iteration, i.e.,
of the previous iteration, i.e.,
![]() . However, for this study, the weighting was used only to
increase accuracy at low frequencies relative to high frequencies.
Weighted equation-error minimization is implemented in the matlab function
invfreqz() (§8.6.4).
. However, for this study, the weighting was used only to
increase accuracy at low frequencies relative to high frequencies.
Weighted equation-error minimization is implemented in the matlab function
invfreqz() (§8.6.4).
The open-hole discrete-time filter was designed using Kopec's method [297], [428, p. 46] in conjunction with weighted equation-error minimization. Kopec's method is based on linear prediction:
- Given a desired complex frequency response
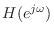 , compute an
allpole model
, compute an
allpole model
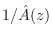 using linear prediction
using linear prediction
- Compute the error spectrum
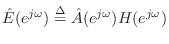 .
.
- Compute an allpole model
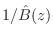 for
for
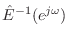 by
minimizing
by
minimizing
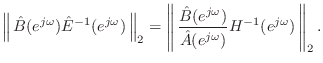
![\includegraphics[width=\twidth]{eps/twoptfilts}](http://www.dsprelated.com/josimages_new/pasp/img2522.png) |
The reasonably close match in both phase and magnitude by second-order filters indicates that there is in fact only one important tonehole resonance and/or anti-resonance within the audio band, and that the measured frequency responses can be modeled with very high audio accuracy using only second-order filters.
Figure 9.50 plots the reflection function calculated for a six-hole flute bore, as described in [240].
![\includegraphics[width=\twidth]{eps/gtwoport}](http://www.dsprelated.com/josimages_new/pasp/img2523.png) |
The Tonehole as a Two-Port Loaded Junction
It seems reasonable to expect that the tonehole should be
representable as a load along a waveguide bore model, thus
creating a loaded two-port junction with two identical bore ports on
either side of the tonehole. From the relations for the loaded
parallel junction (C.101), in the two-port case
with
![]() , and considering pressure waves rather than force
waves, we have
, and considering pressure waves rather than force
waves, we have
| (10.63) | |||
| (10.64) | |||
| (10.65) |
Thus, the loaded two-port junction can be implemented in ``one-filter form'' as shown in Fig. 9.48 with

Each series impedance ![]() in the split-T model of
Fig. 9.43 can be modeled as a series waveguide
junction with a load of
in the split-T model of
Fig. 9.43 can be modeled as a series waveguide
junction with a load of ![]() . To see this, set the transmission
matrix parameters in (9.55) to the values
. To see this, set the transmission
matrix parameters in (9.55) to the values
![]() ,
,
![]() , and
, and ![]() from (9.51) to get
from (9.51) to get
| (10.66) |
where
| (10.67) |
Next we convert pressure to velocity using
| (10.68) |
Finally, we toggle the reference direction of port 2 (the ``current'' arrow for
| (10.69) |
where
Next Section:
Digital Waveguide Bowed-String
Previous Section:
Single-Reed Theory








![\includegraphics[scale=0.9]{eps/fFingerHoleKeefe}](http://www.dsprelated.com/josimages_new/pasp/img2398.png)
![$\displaystyle \left[\begin{array}{c} P_1 \\ [2pt] U_1 \end{array}\right]$](http://www.dsprelated.com/josimages_new/pasp/img2401.png)
![$\displaystyle \left[\begin{array}{cc} 1 & R_a/2 \\ [2pt] 0 & 1 \end{array}\righ...
...1 \end{array}\right]
\left[\begin{array}{c} P_2 \\ [2pt] U_2 \end{array}\right]$](http://www.dsprelated.com/josimages_new/pasp/img2402.png)
![$\displaystyle \left[\begin{array}{cc} 1+\frac{R_a}{2R_s} & R_a[1+\frac{R_a}{4R_...
...} \end{array}\right]
\left[\begin{array}{c} P_2 \\ [2pt] U_2 \end{array}\right]$](http://www.dsprelated.com/josimages_new/pasp/img2403.png)
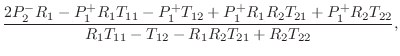
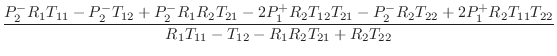
![$\displaystyle \left[\begin{array}{c} P_1^{-} \\ [2pt] P_2^{+} \end{array}\right]$](http://www.dsprelated.com/josimages_new/pasp/img2459.png)
![$\displaystyle \left[\begin{array}{cc} S & T \\ [2pt] T & S \end{array}\right]
\left[\begin{array}{c} P_1^{+} \\ [2pt] P_2^{-} \end{array}\right]$](http://www.dsprelated.com/josimages_new/pasp/img2460.png)
![$\displaystyle \quad
\left[\begin{array}{cc} 4R_aR_s + R_a^2 - 4R_0^2 & 8R_0R_s ...
...rray}\right]
\left[\begin{array}{c} P_1^{+} \\ [2pt] P_2^{-} \end{array}\right]$](http://www.dsprelated.com/josimages_new/pasp/img2462.png)
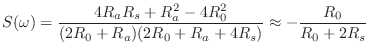
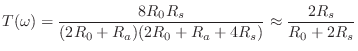
![\includegraphics[scale=0.9]{eps/fFingerHoleScat}](http://www.dsprelated.com/josimages_new/pasp/img2465.png)
![\includegraphics[scale=0.9]{eps/fFingerHoleOneMul}](http://www.dsprelated.com/josimages_new/pasp/img2485.png)
![\includegraphics[scale=0.9]{eps/fFingerHoleOneMulAlt}](http://www.dsprelated.com/josimages_new/pasp/img2486.png)
![\includegraphics[width=\twidth]{eps/fFingerHoleOneMulAltCommuted}](http://www.dsprelated.com/josimages_new/pasp/img2488.png)