DSPRelated.com
Free Books
   Free Books    Physical Audio Signal Processing  

``Traveling Waves'' in Lumped Systems

One of the topics in classical network theory is the reflection and transmission, or scattering formulation for lumped networks [35]. Lumped scattering theory also serves as the starting point for deriving wave digital filters (the subject of Appendix F). In this formulation, forces (voltages) and velocities (currents) are replaced by so-called wave variables

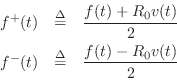
\begin{eqnarray*} f^{{+}}(t) &\isdef & \frac{f(t) + R_0v(t)}{2} \\ f^{{-}}(t) &\isdef & \frac{f(t) - R_0v(t)}{2} \end{eqnarray*}

where $ R_0$ is an arbitrary reference impedance. Since the above wave variables have dimensions of force, they are specifically force waves. The corresponding velocity waves are

\begin{eqnarray*} v^{+}(t) &\isdef & \frac{1}{2}[v(t) + f(t)/R_0], \\ v^{-}(t) &\isdef & \frac{1}{2}[v(t) - f(t)/R_0]. \end{eqnarray*}

Dropping the time argument, since it is always `(t)', we see that

$\displaystyle f^{{+}}$ $\displaystyle =$ $\displaystyle R_0v^{+}$  
$\displaystyle f^{{-}}$ $\displaystyle =$ $\displaystyle -R_0v^{-}\protect$ (C.73)

and
$\displaystyle f$ $\displaystyle =$ $\displaystyle f^{{+}}+ f^{{-}}$  
$\displaystyle v$ $\displaystyle =$ $\displaystyle v^{+}+ v^{-}\protect$ (C.74)

These are the basic relations for traveling waves in an ideal medium such as an ideal vibrating string or acoustic tube. Using voltage and current gives elementary transmission line theory.

Reflectance of an Impedance

Let $ R(s)$ denote the driving-point impedance of an arbitrary continuous-time LTI system. Then, by definition, $ F(s)=R(s)V(s)$ where $ F(s)$ and $ V(s)$ denote the Laplace transforms of the applied force and resulting velocity, respectively. The wave variable decomposition in Eq.$ \,$(C.74) gives

$\displaystyle F(s)$ $\displaystyle =$ $\displaystyle R(s) V(s)$  
$\displaystyle \,\,\Rightarrow\,\,F^{+}(s) + F^{-}(s)$ $\displaystyle =$ $\displaystyle R(s) \left[V^{+}(s) + V^{-}(s)\right]$  
  $\displaystyle =$ $\displaystyle R(s) \left[\frac{F^{+}(s) - F^{-}(s)}{R_0}\right]$  
$\displaystyle \,\,\Rightarrow\,\,F^{-}(s) \left[\frac{R(s)}{R_0}+1\right]$ $\displaystyle =$ $\displaystyle F^{+}(s) \left[\frac{R(s)}{R_0}-1\right]$  
$\displaystyle \,\,\Rightarrow\,\,F^{-}(s)$ $\displaystyle =$ $\displaystyle F^{+}(s) \left[\frac{R(s)-R_0}{R(s)+R_0}\right]$  
  $\displaystyle \isdef$ $\displaystyle F^{+}(s)\, \hat{\rho}_f(s) \protect$ (C.75)

We may call $ \hat{\rho}_f(s)$ the reflectance of impedance $ R(s)$ relative to $ R_0$. For example, if a transmission line with characteristic impedance $ R_0$ were terminated in a lumped impedance $ R(s)$, the reflection transfer function at the termination, as seen from the end of the transmission line, would be $ \hat{\rho}_f(s)$.

We are working with reflectance for force waves. Using the elementary relations Eq.$ \,$(C.73), i.e., $ F^{+}(s) = R_0V^{+}(s)$ and $ F^{-}(s) = -R_0V^{-}(s)$, we immediately obtain the corresponding velocity-wave reflectance:

$\displaystyle \hat{\rho}_v(s) \isdefs \frac{V^{-}(s)}{V^{+}(s)} \eqsp \frac{-F^... .../R_0}{F^{+}(s)/R_0} \eqsp - \frac{F^{-}(s)}{F^{+}(s)} \eqsp - \hat{\rho}_f(s) $

Next Section:
Properties of Passive Impedances
Previous Section:
Digital Waveguide Filters