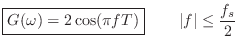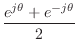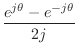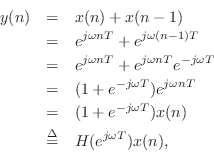DSPRelated.com
Free Books
   Free Books    Introduction to Digital Filters  

The Simplest Lowpass Filter

This chapter introduces analysis of digital filters applied to a very simple example filter. The initial treatment uses only high-school level math (trigonometry), followed by an easier but more advanced approach using complex variables. Several important topics in digital signal processing are introduced in an extremely simple setting, and motivation is given for the study of further topics such as complex variables and Fourier analysis [84].

Introduction

Musicians have been using filters for thousands of years to shape the sounds of their art in various ways. For example, the evolution of the physical dimensions of the violin constitutes an evolution in filter design. The choice of wood, the shape of the cutouts, the geometry of the bridge, and everything that affects resonance all have a bearing on how the violin body filters the signal induced at the bridge by the vibrating strings. Once a sound is airborne there is yet more filtering performed by the listening environment, by the pinnae of the ear, and by idiosyncrasies of the hearing process.

What is a Filter?

Any medium through which the music signal passes, whatever its form, can be regarded as a filter. However, we do not usually think of something as a filter unless it can modify the sound in some way. For example, speaker wire is not considered a filter, but the speaker is (unfortunately). The different vowel sounds in speech are produced primarily by changing the shape of the mouth cavity, which changes the resonances and hence the filtering characteristics of the vocal tract. The tone control circuit in an ordinary car radio is a filter, as are the bass, midrange, and treble boosts in a stereo preamplifier. Graphic equalizers, reverberators, echo devices, phase shifters, and speaker crossover networks are further examples of useful filters in audio. There are also examples of undesirable filtering, such as the uneven reinforcement of certain frequencies in a room with ``bad acoustics.'' A well-known signal processing wizard is said to have remarked, ``When you think about it, everything is a filter.''

A digital filter is just a filter that operates on digital signals, such as sound represented inside a computer. It is a computation which takes one sequence of numbers (the input signal) and produces a new sequence of numbers (the filtered output signal). The filters mentioned in the previous paragraph are not digital only because they operate on signals that are not digital. It is important to realize that a digital filter can do anything that a real-world filter can do. That is, all the filters alluded to above can be simulated to an arbitrary degree of precision digitally. Thus, a digital filter is only a formula for going from one digital signal to another. It may exist as an equation on paper, as a small loop in a computer subroutine, or as a handful of integrated circuit chips properly interconnected.

Why learn about filters?

Computer musicians nearly always use digital filters in every piece of music they create. Without digital reverberation, for example, it is difficult to get rich, full-bodied sound from the computer. However, reverberation is only a surface scratch on the capabilities of digital filters. A digital filter can arbitrarily shape the spectrum of a sound. Yet very few musicians are prepared to design the filter they need, even when they know exactly what they want in the way of a spectral modification. A goal of this book is to assist sound designers by listing the concepts and tools necessary for doing custom filter designs.

There is plenty of software available for designing digital filters [10,8,22]. In light of this available code, it is plausible to imagine that only basic programming skills are required to use digital filters. This is perhaps true for simple applications, but knowledge of how digital filters work will help at every phase of using such software.

Also, you must understand a program before you can modify it or extract pieces of it. Even in standard applications, effective use of a filter design program requires an understanding of the design parameters, which in turn requires some understanding of filter theory. Perhaps most important for composers who design their own sounds, a vast range of imaginative filtering possibilities is available to those who understand how filters affect sounds. In my practical experience, intimate knowledge of filter theory has proved to be a very valuable tool in the design of musical instruments. Typically, a simple yet unusual filter is needed rather than one of the classical designs obtainable using published software.


The Simplest Lowpass Filter

Let's start with a very basic example of the generic problem at hand: understanding the effect of a digital filter on the spectrum of a digital signal. The purpose of this example is to provide motivation for the general theory discussed in later chapters.

Figure 1.1: Amplitude response (gain versus frequency) specification for the ideal low-pass filter.
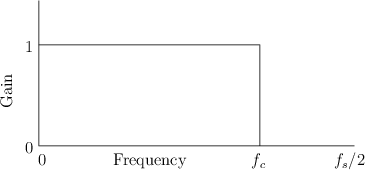
\begin{figure}\input fig/kfigtpone.pstex_t \end{figure}

Our example is the simplest possible low-pass filter. A low-pass filter is one which does not affect low frequencies and rejects high frequencies. The function giving the gain of a filter at every frequency is called the amplitude response (or magnitude frequency response). The amplitude response of the ideal lowpass filter is shown in Fig.1.1. Its gain is 1 in the passband, which spans frequencies from 0 Hz to the cut-off frequency $ f_c$ Hz, and its gain is 0 in the stopband (all frequencies above $ f_c$). The output spectrum is obtained by multiplying the input spectrum by the amplitude response of the filter. In this way, signal components are eliminated (``stopped'') at all frequencies above the cut-off frequency, while lower-frequency components are ``passed'' unchanged to the output.

Definition of the Simplest Low-Pass

The simplest (and by no means ideal) low-pass filter is given by the following difference equation:

$\displaystyle y(n) = x(n) + x(n - 1) \protect$ (2.1)

where $ x(n)$ is the filter input amplitude at time (or sample) $ n$, and $ y(n)$ is the output amplitude at time $ n$. The signal flow graph (or simulation diagram) for this little filter is given in Fig.1.2. The symbol ``$ z^{-1}$'' means a delay of one sample, i.e., $ z^{-1}x(n) = x(n - 1)$.

Figure 1.2: System diagram for the filter $ y(n) = x(n) + x(n - 1)$.
\begin{figure}\input fig/kfig2p2.pstex_t \end{figure}

It is important when working with spectra to be able to convert time from sample-numbers, as in Eq.$ \,$(1.1) above, to seconds. A more ``physical'' way of writing the filter equation is

$\displaystyle y(nT) = x(nT) + x[(n - 1)T]\qquad n = 0, 1, 2, \ldots\,, $

where $ T$ is the sampling interval in seconds. It is customary in digital signal processing to omit $ T$ (set it to 1), but anytime you see an $ n$ you can translate to seconds by thinking $ nT$. Be careful with integer expressions, however, such as $ (n - k)$, which would be $ (n-k)T$ seconds, not $ (nT - k)$. Further discussion of signal representation and notation appears in §A.1.

To further our appreciation of this example, let's write a computer subroutine to implement Eq.$ \,$(1.1). In the computer, $ x(n)$ and $ y(n)$ are data arrays and $ n$ is an array index. Since sound files may be larger than what the computer can hold in memory all at once, we typically process the data in blocks of some reasonable size. Therefore, the complete filtering operation consists of two loops, one within the other. The outer loop fills the input array $ x$ and empties the output array $ y$, while the inner loop does the actual filtering of the $ x$ array to produce $ y$. Let $ M$ denote the block size (i.e., the number of samples to be processed on each iteration of the outer loop). In the C programming language, the inner loop of the subroutine might appear as shown in Fig.1.3. The outer loop might read something like ``fill $ x$ from the input file,'' ``call simplp,'' and ``write out $ y$.''

Figure: Implementation of the simple low-pass filter of Eq.$ \,$(1.1) in the C programming language.
  
/* C function implementing the simplest lowpass:
 *
 *      y(n) = x(n) + x(n-1)
 *
 */
double simplp (double *x, double *y,
               int M, double xm1)
{
  int n;
  y[0] = x[0] + xm1;
  for (n=1; n < M ; n++) {
    y[n] =  x[n]  + x[n-1];
  }
  return x[M-1];
}

In this implementation, the first instance of $ x(n-1)$ is provided as the procedure argument xm1. That way, both $ x$ and $ y$ can have the same array bounds ( $ 0,\dots,M-1$). For convenience, the value of xm1 appropriate for the next call to simplp is returned as the procedure's value.

We may call xm1 the filter's state. It is the current ``memory'' of the filter upon calling simplp. Since this filter has only one sample of state, it is a first order filter. When a filter is applied to successive blocks of a signal, it is necessary to save the filter state after processing each block. The filter state after processing block $ m$ is then the starting state for block $ m+1$.

Figure 1.4 illustrates a simple main program which calls simplp. The length 10 input signal x is processed in two blocks of length 5.

Figure 1.4: C main program for calling the simple low-pass filter simplp
  
/* C main program for testing simplp */
main() {
  double x[10] = {1,2,3,4,5,6,7,8,9,10};
  double y[10];

  int i;
  int N=10;
  int M=N/2; /* block size */
  double xm1 = 0;

  xm1 = simplp(x, y, M, xm1);
  xm1 = simplp(&x[M], &y[M], M, xm1);

  for (i=0;i<N;i++) {
    printf("x[%d]=%f\ty[%d]=%f\n",i,x[i],i,y[i]);
  }
  exit(0);
}
/* Output:
 *    x[0]=1.000000     y[0]=1.000000
 *    x[1]=2.000000     y[1]=3.000000
 *    x[2]=3.000000     y[2]=5.000000
 *    x[3]=4.000000     y[3]=7.000000
 *    x[4]=5.000000     y[4]=9.000000
 *    x[5]=6.000000     y[5]=11.000000
 *    x[6]=7.000000     y[6]=13.000000
 *    x[7]=8.000000     y[7]=15.000000
 *    x[8]=9.000000     y[8]=17.000000
 *    x[9]=10.000000    y[9]=19.000000
 */

You might suspect that since Eq.$ \,$(1.1) is the simplest possible low-pass filter, it is also somehow the worst possible low-pass filter. How bad is it? In what sense is it bad? How do we even know it is a low-pass at all? The answers to these and related questions will become apparent when we find the frequency response of this filter.

Finding the Frequency Response

Think of the filter expressed by Eq.$ \,$(1.1) as a ``black box'' as depicted in Fig.1.5. We want to know the effect of this black box on the spectrum of $ x(\cdot)$, where $ x(\cdot)$ represents the entire input signal (see §A.1).

Figure 1.5: ``Black box'' representation of an arbitrary filter
\begin{figure}\input fig/kfig2p3.pstex_t \end{figure}

Sine-Wave Analysis

Suppose we test the filter at each frequency separately. This is called sine-wave analysis.2.1Fig.1.6 shows an example of an input-output pair, for the filter of Eq.$ \,$(1.1), at the frequency $ f=f_s/4$ Hz, where $ f_s$ denotes the sampling rate. (The continuous-time waveform has been drawn through the samples for clarity.) Figure 1.6a shows the input signal, and Fig.1.6b shows the output signal.

Figure 1.6: Input and output signals for the filter $ y(n) = x(n) + x(n - 1)$. (a) Input sinusoid $ x(n) = A_1 \sin(2\pi f n T + \phi_1)$ at amplitude $ A_1=1$, frequency $ f=f_s/4$, and phase $ \phi _1=0$. (b) Output sinusoid $ y(n) = A_2 \sin(2\pi f nT + \phi_2)$ at amplitude $ A_2=1.414$, frequency $ f=f_s/4$, and phase $ \phi _2 = - \pi /4$.
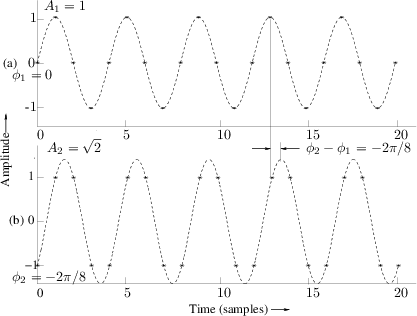\begin{figure}\input fig/kfig2p4.pstex_t \end{figure}

The ratio of the peak output amplitude to the peak input amplitude is the filter gain at this frequency. From Fig.1.6 we find that the gain is about 1.414 at the frequency $ f_s/4$. We may also say the amplitude response is 1.414 at $ f_s/4$.

The phase of the output signal minus the phase of the input signal is the phase response of the filter at this frequency. Figure 1.6 shows that the filter of Eq.$ \,$(1.1) has a phase response equal to $ -2\pi/8$ (minus one-eighth of a cycle) at the frequency $ f=f_s/4$.

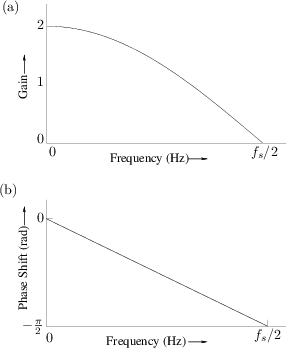
Continuing in this way, we can input a sinusoid at each frequency (from 0 to $ f_s/2$ Hz), examine the input and output waveforms as in Fig.1.6, and record on a graph the peak-amplitude ratio (gain) and phase shift for each frequency. The resultant pair of plots, shown in Fig.1.7, is called the frequency response. Note that Fig.1.6 specifies the middle point of each graph in Fig.1.7.

Not every black box has a frequency response, however. What good is a pair of graphs such as shown in Fig.1.7 if, for all input sinusoids, the output is 60 Hz hum? What if the output is not even a sinusoid? We will learn in Chapter 4 that the sine-wave analysis procedure for measuring frequency response is meaningful only if the filter is linear and time-invariant (LTI). Linearity means that the output due to a sum of input signals equals the sum of outputs due to each signal alone. Time-invariance means that the filter does not change over time. We will elaborate on these technical terms and their implications later. For now, just remember that LTI filters are guaranteed to produce a sinusoid in response to a sinusoid--and at the same frequency.

Figure 1.7: Frequency response for the filter $ y(n) = x(n) + x(n - 1)$. (a) Amplitude response. (b) Phase response.
\begin{figure}\input fig/kfig2p5.pstex_t \end{figure}

Mathematical Sine-Wave Analysis

The above method of finding the frequency response involves physically measuring the amplitude and phase response for input sinusoids of every frequency. While this basic idea may be practical for a real black box at a selected set of frequencies, it is hardly useful for filter design. Ideally, we wish to arrive at a mathematical formula for the frequency response of the filter given by Eq.$ \,$(1.1). There are several ways of doing this. The first we consider is exactly analogous to the sine-wave analysis procedure given above.

Assuming Eq.$ \,$(1.1) to be a linear time-invariant filter specification (which it is), let's take a few points in the frequency response by analytically ``plugging in'' sinusoids at a few different frequencies. Two graphs are required to fully represent the frequency response: the amplitude response (gain versus frequency) and phase response (phase shift versus frequency).

The frequency 0 Hz (often called dc, for direct current) is always comparatively easy to handle when we analyze a filter. Since plugging in a sinusoid means setting $ x(n) = A \cos(2\pi fnT + \phi )$, by setting $ f = 0$, we obtain $ x(n) = A \cos[2\pi(0)T + \phi] = A \cos(\phi)$ for all $ n$. The input signal, then, is the same number $ (A \cos(\phi))$ over and over again for each sample. It should be clear that the filter output will be $ y(n) = x(n) + x(n - 1) = A \cos(\phi) + A \cos(\phi) = 2A \cos(\phi)$ for all $ n$. Thus, the gain at frequency $ f = 0$ is 2, which we get by dividing $ 2A$, the output amplitude, by $ A$, the input amplitude.

Phase has no effect at $ f = 0$ Hz because it merely shifts a constant function to the left or right. In cases such as this, where the phase response may be arbitrarily defined, we choose a value which preserves continuity. This means we must analyze at frequencies in a neighborhood of the arbitrary point and take a limit. We will compute the phase response at dc later, using different techniques. It is worth noting, however, that at 0 Hz, the phase of every real2.2 linear time-invariant system is either 0 or $ \pi $, with the phase $ \pi $ corresponding to a sign change. The phase of a complex filter at dc may of course take on any value in $ [-\pi ,\pi )$.

The next easiest frequency to look at is half the sampling rate, $ f= f_s/2 = 1/(2T)$. In this case, using basic trigonometry (see §A.2), we can simplify the input $ x$ as follows:

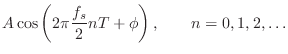$\displaystyle x(n)$ $\displaystyle =$ $\displaystyle A \cos\left(2\pi\frac{f_s}{2} n T + \phi\right), \qquad n = 0, 1, 2,\ldots$  
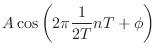  $\displaystyle =$ $\displaystyle A \cos\left(2\pi\frac{1}{2T} n T + \phi\right)$  
  $\displaystyle =$ $\displaystyle A \cos(\pi n + \phi)$  
  $\displaystyle =$ $\displaystyle A \cos(\pi n)\cos(\phi) - A\sin(\pi n)\sin(\phi)$  
  $\displaystyle =$ $\displaystyle A \cos(\pi n)\cos(\phi)$  
  $\displaystyle =$ $\displaystyle A (-1)^n\cos(\phi), \qquad n = 0, 1, 2,\ldots$  
  $\displaystyle =$ $\displaystyle [A\cos(\phi), -A\cos(\phi), A\cos(\phi), -A\cos(\phi), \ldots],$ (2.2)

where the beginning of time was arbitrarily set at $ n = 0$. Now with this input, the output of Eq.$ \,$(1.1) is
$\displaystyle y(n)$ $\displaystyle =$ $\displaystyle x(n) + x(n - 1)$  
  $\displaystyle =$ $\displaystyle (-1)^n A \cos(\phi) + (-1)^{n-1} A \cos(\phi)$  
  $\displaystyle =$ $\displaystyle (-1)^n A \cos(\phi) - (-1)^n A \cos(\phi)$  
  $\displaystyle =$ $\displaystyle 0.$ (2.3)

The filter of Eq.$ \,$(1.1) thus has a gain of 0 at $ f=f_s/2$. Again the phase is not measurable, since the output signal is identically zero. We will again need to extrapolate the phase response from surrounding frequencies (which will be done in §7.6.1).

If we back off a bit, the above results for the amplitude response are obvious without any calculations. The filter $ y(n) = x(n) + x(n - 1)$ is equivalent (except for a factor of 2) to a simple two-point average, $ y(n) = [x(n) + x(n - 1)]/ 2$. Averaging adjacent samples in a signal is intuitively a low-pass filter because at low frequencies the sample amplitudes change slowly, so that the average of two neighboring samples is very close to either sample, while at high frequencies the adjacent samples tend to have opposite sign and to cancel out when added. The two extremes are frequency 0 Hz, at which the averaging has no effect, and half the sampling rate $ f_s/2$ where the samples alternate in sign and exactly add to 0.

We are beginning to see that Eq.$ \,$(1.1) may be a low-pass filter after all, since we found a boost of about 6 dB at the lowest frequency and a null at the highest frequency. (A gain of 2 may be expressed in decibels as $ 20\log_{10}(2) \approx 6.02$ dB, and a null or notch is another term for a gain of 0 at a single frequency.) Of course, we tried only two out of an infinite number of possible frequencies.

Let's go for broke and plug the general sinusoid into Eq.$ \,$(1.1), confident that a table of trigonometry identities will see us through (after all, this is the simplest filter there is, right?). To set the input signal to a completely arbitrary sinusoid at amplitude $ A$, phase $ \phi$, and frequency $ f$ Hz, we let $ x(n) = A \cos(2\pi fnT + \phi )$. The output is then given by

$\displaystyle y(n) = A \cos(2\pi f n T + \phi ) + A \cos[2\pi f(n - 1)T + \phi]. $

This input can be simplified as follows: Recall from the discussion surrounding Fig.1.6 that only the peak-amplitude ratio and the phase difference between input and output sinusoids are needed to measure the frequency response. The filter phase response does not depend on $ \phi$ above (due to time-invariance), and so we can set $ \phi$ to 0. Also, the filter amplitude response does not depend on $ A$ (due to linearity), so we let $ A = 1$. With these simplifications of $ x(n)$, the gain and phase response of the filter will appear directly as the amplitude and phase of the output $ y(n)$. Thus, we input the signal

$\displaystyle x(n) = \cos(2\pi f n T) = \cos(\omega nT), $

where $ \omega \isdef 2\pi f$, as discussed in §A.1. (The symbol $ \isdef $ means ``is defined as''.) With this input, the output of the simple low-pass filter is given by

$\displaystyle y(n) = \cos(\omega nT) + \cos[\omega(n - 1)T]. $

All that remains is to reduce the above expression to a single sinusoid with some frequency-dependent amplitude and phase. We do this first by using standard trigonometric identities [2] in order to avoid introducing complex numbers. Next, a much ``easier'' derivation using complex numbers will be given.

Note that a sum of sinusoids at the same frequency, but possibly different phase and amplitude, can always be expressed as a single sinusoid at that frequency with some resultant phase and amplitude. While we find this result by direct derivation in working out our simple example, the general case is derived in §A.3 for completeness.

We have

$\displaystyle y(n)$ $\displaystyle =$ $\displaystyle \cos(\omega nT) + \cos[\omega(n - 1)T]$  
  $\displaystyle =$ $\displaystyle \cos(\omega nT) + \cos(\omega nT) \cos(-\omega T) - \sin(\omega nT) \sin(-\omega T)$  
  $\displaystyle =$ $\displaystyle \cos(\omega nT) + \cos(\omega nT) \cos(\omega T) + \sin(\omega nT) \sin(\omega T)$  
  $\displaystyle =$ $\displaystyle \left[1 + \cos(\omega T)\right] \cos(\omega nT) + \sin(\omega T) \sin(\omega n T)$  
  $\displaystyle =$ $\displaystyle a(\omega) \cos(\omega nT) + b(\omega) \sin(\omega nT)$ (2.4)

where $ a(\omega)\isdef [1 + \cos(\omega T)]$ and $ b(\omega) \isdef \sin(\omega T)$. We are looking for an answer of the form

$\displaystyle y(n) = G(\omega) \cos\left[\omega nT + \Theta(\omega)\right], $

where $ G(\omega)$ is the filter amplitude response and $ \Theta(\omega)$ is the phase response. This may be expanded as

$\displaystyle y(n) = G(\omega) \cos\left[\Theta(\omega)\right] \cos(\omega nT) - G(\omega) \sin[\Theta(\omega)] \sin(\omega n T). $

Therefore,
$\displaystyle a(\omega)$ $\displaystyle =$ $\displaystyle \quad\! G(\omega) \cos\left[\Theta(\omega)\right]$  
$\displaystyle b(\omega)$ $\displaystyle =$ $\displaystyle - G(\omega) \sin\left[\Theta(\omega)\right]. \protect$ (2.5)

Amplitude Response

We can isolate the filter amplitude response $ G(\omega)$ by squaring and adding the above two equations:

\begin{eqnarray*} a^2(\omega) + b^2(\omega) &=& G^2(\omega)\cos^2[\Theta(\omega)... ...ta(\omega)] + \sin^2[\Theta(\omega)]\right\}\\ &=& G^2(\omega). \end{eqnarray*}

This can then be simplified as follows:

\begin{eqnarray*} G^2(\omega) &=& a^2(\omega) + b^2(\omega)\\ &=& [1 + \cos(\... ... \cos(\omega T) \\ &=&4 \cos^2\left(\frac{\omega T}{2}\right). \end{eqnarray*}

So we have made it to the amplitude response of the simple lowpass filter $ y(n) = x(n) + x(n - 1)$:

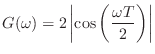
$\displaystyle G(\omega) = 2 \left\vert\cos\left(\frac{\omega T}{2}\right)\right\vert $

Since $ \cos(\pi fT)$ is nonnegative for $ -f_s/2 \leq f \leq f_s/2$, it is unnecessary to take the absolute value as long as $ f$ is understood to lie in this range:

$\displaystyle \zbox {G(\omega) = 2 \cos(\pi f T)} \qquad \left\vert f\right\vert \leq \frac{f_s}{2} \protect$ (2.6)

Phase Response

Now we may isolate the filter phase response $ \Theta(\omega)$ by taking a ratio of the $ a(\omega)$ and $ b(\omega)$ in Eq.$ \,$(1.5):

\begin{eqnarray*} \frac{b(\omega)}{a(\omega)} &=& -\frac{G(\omega) \sin\left[\... ...eft[\Theta(\omega)\right]}\\ &\isdef & - \tan[\Theta(\omega)] \end{eqnarray*}

Substituting the expansions of $ a(\omega)$ and $ b(\omega)$ yields

\begin{eqnarray*} \tan[\Theta(\omega)] &=& - \frac{b(\omega)}{a(\omega)} \\ &=&... ...n(\omega T/2)}{\cos(\omega T/2)} = \tan\left(-\omega T/2\right). \end{eqnarray*}

Thus, the phase response of the simple lowpass filter $ y(n) = x(n) + x(n - 1)$ is

$\displaystyle \zbox {\Theta(\omega) = -\omega T/2.} \protect$ (2.7)

We have completely solved for the frequency response of the simplest low-pass filter given in Eq.$ \,$(1.1) using only trigonometric identities. We found that an input sinusoid of the form

$\displaystyle x(n) = A \cos(2\pi fnT + \phi) $

produces the output

$\displaystyle y(n) = 2A \cos(\pi f T) \cos(2\pi fnT + \phi - \pi fT). $

Thus, the gain versus frequency is $ 2\cos(\pi fT)$ and the change in phase at each frequency is given by $ -\pi fT$ radians. These functions are shown in Fig.1.7. With these functions at our disposal, we can predict the filter output for any sinusoidal input. Since, by Fourier theory [84], every signal can be represented as a sum of sinusoids, we've also solved the more general problem of predicting the output given any input signal.

An Easier Way

We derived the frequency response above using trig identities in order to minimize the mathematical level involved. However, it turns out it is actually easier, though more advanced, to use complex numbers for this purpose. To do this, we need Euler's identity:

$\displaystyle \zbox {e^{j\theta} = \cos(\theta) + j \sin(\theta)}\qquad \hbox{(Euler's Identity)} \protect$ (2.8)

where $ j\isdef \sqrt{-1}$ is the imaginary unit for complex numbers, and $ e$ is a transcendental constant approximately equal to $ 2.718\ldots$. Euler's identity is fully derived in [84]; here we will simply use it ``on faith.'' It can be proved by computing the Taylor series expansion of each side of Eq.$ \,$(1.8) and showing equality term by term [84,14].

Complex Sinusoids

Using Euler's identity to represent sinusoids, we have

$\displaystyle A e^{j(\omega t+\phi)} = A\cos(\omega t+\phi) + j A\sin(\omega t+\phi) \protect$ (2.9)

when time $ t$ is continuous (see §A.1 for a list of notational conventions), and when time is discrete,

$\displaystyle A e^{j(\omega nT+\phi)} = A\cos(\omega nT+\phi) + j A\sin(\omega nT+\phi). \protect$ (2.10)

Any function of the form $ A e^{j(\omega t+\phi)}$ or $ A e^{j(\omega nT+\phi)}$ will henceforth be called a complex sinusoid.2.3 We will see that it is easier to manipulate both sine and cosine simultaneously in this form than it is to deal with either sine or cosine separately. One may even take the point of view that $ e^{j\theta}$ is simpler and more fundamental than $ \sin(\theta)$ or $ \cos(\theta)$, as evidenced by the following identities (which are immediate consequences of Euler's identity, Eq.$ \,$(1.8)):

$\displaystyle \cos(\theta)$ $\displaystyle =$ $\displaystyle \frac{e^{j\theta} + e^{-j\theta}}{2} \protect$ (2.11)
$\displaystyle \sin(\theta)$ $\displaystyle =$ $\displaystyle \frac{e^{j\theta} - e^{-j\theta}}{2j} \protect$ (2.12)

Thus, sine and cosine may each be regarded as a combination of two complex sinusoids. Another reason for the success of the complex sinusoid is that we will be concerned only with real linear operations on signals. This means that $ j$ in Eq.$ \,$(1.8) will never be multiplied by $ j$ or raised to a power by a linear filter with real coefficients. Therefore, the real and imaginary parts of that equation are actually treated independently. Thus, we can feed a complex sinusoid into a filter, and the real part of the output will be the cosine response and the imaginary part of the output will be the sine response. For the student new to analysis using complex variables, natural questions at this point include ``Why $ e$?, Where did the imaginary exponent come from? Are imaginary exponents legal?'' and so on. These questions are fully answered in [84] and elsewhere [53,14]. Here, we will look only at some intuitive connections between complex sinusoids and the more familiar real sinusoids.

Complex Amplitude

Note that the amplitude $ A$ and phase $ \phi$ can be viewed as the magnitude and angle of a single complex number

$\displaystyle {\cal A}\isdefs A e^{j\phi} $

which is naturally thought of as the complex amplitude of the complex sinusoid defined by the left-hand side of either Eq.$ \,$(1.9) or Eq.$ \,$(1.10). The complex amplitude is the same whether we are talking about the continuous-time sinusoid $ A e^{j(\omega t+\phi)}$ or the discrete-time sinusoid $ A e^{j(\omega nT+\phi)}$.

Phasor Notation

The complex amplitude $ {\cal A}\isdef A e^{j\phi}$ is also defined as the phasor associated with any sinusoid having amplitude $ A$ and phase $ \phi$. The term ``phasor'' is more general than ``complex amplitude'', however, because it also applies to the corresponding real sinusoid given by the real part of Equations (1.9-1.10). In other words, the real sinusoids $ A\cos(\omega t+\phi)$ and $ A\cos(\omega nT+\phi)$ may be expressed as

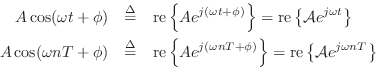
\begin{eqnarray*} A\cos(\omega t+\phi) &\isdef & \mbox{re}\left\{A e^{j(\omega t... ...hi)}\right\} = \mbox{re}\left\{{\cal A}e^{j\omega nT}\right\}\\ \end{eqnarray*}

and $ {\cal A}$ is the associated phasor in each case. Thus, we say that the phasor representation of $ A\cos(\omega t+\phi)$ is $ {\cal A}\isdef A e^{j\phi}$. Phasor analysis is often used to analyze linear time-invariant systems such as analog electrical circuits.

Plotting Complex Sinusoids as Circular Motion

Figure 1.8 shows Euler's relation graphically as it applies to sinusoids. A point traveling with uniform velocity around a circle with radius 1 may be represented by $ e^{j\omega t}=e^{j2\pi f t}$ in the complex plane, where $ t$ is time and $ f$ is the number of revolutions per second. The projection of this motion onto the horizontal (real) axis is $ \cos (\omega t)$, and the projection onto the vertical (imaginary) axis is $ \sin (\omega t)$. For discrete-time circular motion, replace $ t$ by $ nT$ to get $ e^{j\omega nT} = e^{j2\pi (f/f_s) n}$ which may be interpreted as a point which jumps an arc length $ 2\pi f/f_s$ radians along the circle each sampling instant.

Figure: Relation of uniform circular motion to sinusoidal motion via Euler's identity $ \exp (j\omega t) = \cos (\omega t) + j\sin (\omega t)$ (Eq.$ \,$(1.8)). The projection of $ \exp (j\omega t)$ onto the real axis is $ \cos (\omega t)$, and its projection onto the imaginary axis is $ \sin (\omega t)$.
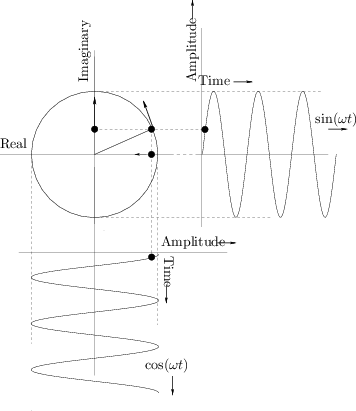\begin{figure}\input fig/kfig2p6.pstex_t \end{figure}

Figure 1.9: Opposite circular motions add to give real sinusoidal motion, $ e^{j\omega t} + e^{-j\omega t} = 2\cos (\omega t)$.
\begin{figure}\input fig/kfig2p7.pstex_t \end{figure}

$\textstyle \parbox{0.8\textwidth}{% \emph{Euler's identity says that a complex ... ...otion in the complex plane, and is the vector sum of two sinusoidal motions.} }$

For circular motion to ensue, the sinusoidal motions must be at the same frequency, one-quarter cycle out of phase, and perpendicular (orthogonal) to each other. (With phase differences other than one-quarter cycle, the motion is generally elliptical.)

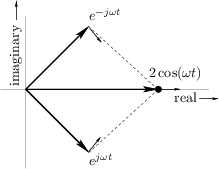
The converse of this is also illuminating. Take the usual circular motion $ e^{j\omega t}$ which spins counterclockwise along the unit circle as $ t$ increases, and add to it a similar but clockwise circular motion $ e^{-j\omega t}$. This is shown in Fig.1.9. Next apply Euler's identity to get

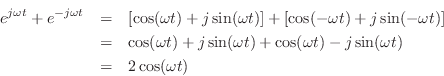
\begin{eqnarray*} e^{j\omega t} + e^{-j\omega t} & = & [\cos(\omega t) + j \sin(... ...a t) + \cos(\omega t) - j \sin(\omega t)\\ &=& 2 \cos(\omega t) \end{eqnarray*}

Thus,

$\textstyle \parbox{0.8\textwidth}{% \emph{\emph{Cosine} motion is the vector sum of two circular motions with the same angular speed but opposite direction.}}$
This statement is a graphical or geometric interpretation of Eq.$ \,$(1.11). A similar derivation (subtracting instead of adding) gives the sine identity Eq.$ \,$(1.12).

We call $ e^{j\omega t}$ a positive-frequency sinusoidal component when $ \omega > 0$, and $ e^{-j\omega t}$ is the corresponding negative-frequency component. Note that both sine and cosine signals have equal-amplitude positive- and negative-frequency components (see also [84,53]). This happens to be true of every real signal (i.e., non-complex). To see this, recall that every signal can be represented as a sum of complex sinusoids at various frequencies (its Fourier expansion). For the signal to be real, every positive-frequency complex sinusoid must be summed with a negative-frequency sinusoid of equal amplitude. In other words, any counterclockwise circular motion must be matched by an equal and opposite clockwise circular motion in order that the imaginary parts always cancel to yield a real signal (see Fig.1.9). Thus, a real signal always has a magnitude spectrum which is symmetric about 0 Hz. Fourier symmetries such as this are developed more completely in [84].

Rederiving the Frequency Response

Let's repeat the mathematical sine-wave analysis of the simplest low-pass filter, but this time using a complex sinusoid instead of a real one. Thus, we will test the filter's response at frequency $ f$ by setting its input to

$\displaystyle x(n) = Ae^{j(2\pi f nT + \phi)} = A\cos(2\pi f n T + \phi) + j A\sin(2\pi f n T + \phi). $

Again, because of time-invariance, the frequency response will not depend on $ \phi$, so let $ \phi = 0$. Similarly, owing to linearity, we may normalize $ A$ to 1. By virtue of Euler's relation Eq.$ \,$(1.8) and the linearity of the filter, setting the input to $ x(n) = e^{j\omega nT}$ is physically equivalent to putting $ \cos(\omega nT)$ into one copy of the filter and $ \sin(\omega nT)$ into a separate copy of the same filter. The signal path where the cosine goes in is the real part of the signal, and the other signal path is simply called the imaginary part. Thus, a complex signal in real life is implemented as two real signals processed in parallel; in particular, a complex sinusoid is implemented as two real sinusoids, side by side, one-quarter cycle out of phase. When the filter itself is real, two copies of it suffice to process a complex signal. If the filter is complex, we must implement complex multiplies between the complex signal samples and filter coefficients.

Using the normal rules for manipulating exponents, we find that the output of the simple low-pass filter in response to the complex sinusoid at frequency $ \omega/2\pi$ Hz is given by

\begin{eqnarray*} y(n) &=& x(n) + x(n - 1) \\ &=& e^{j\omega n T} + e^{j\omeg... ...{-j\omega T}) x(n)\\ &\isdef & H(e^{j\omega T}) x(n), \protect \end{eqnarray*}

where we have defined $ H(e^{j\omega T})\isdef (1+e^{-j\omega T})$, which we will show is in fact the frequency response of this filter at frequency $ \omega$. This derivation is clearly easier than the trigonometry approach. What may be puzzling at first, however, is that the filter is expressed as a frequency-dependent complex multiply (when the input signal is a complex sinusoid). What does this mean? Well, the theory we are blindly trusting at this point says it must somehow mean a gain scaling and a phase shift. This is true and easy to see once the complex filter gain is expressed in polar form,

$\displaystyle H(e^{j\omega T}) \eqsp G(\omega)e^{j\Theta(\omega)}, $

where the gain versus frequency is given by $ G(\omega)\isdef \vert H(e^{j\omega T})\vert$ (the absolute value, or modulus of $ H$), and the phase shift in radians versus frequency is given by the phase angle (or argument) $ \Theta(\omega)\isdeftext \angle H(e^{j\omega T})$. In other words, we must find

$\displaystyle G(\omega) \isdefs \left\vert H(e^{j\omega T})\right\vert $

which is the amplitude response, and

$\displaystyle \Theta(\omega) \isdefs \angle H(e^{j\omega T}) $

which is the phase response. There is a trick we can call ``balancing the exponents,'' which will work nicely for the simple low-pass of Eq.$ \,$(1.1).

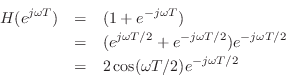
\begin{eqnarray*} H(e^{j\omega T}) &=& (1 + e^{-j\omega T})\\ &=& (e^{j\omega... ... T/2})e^{-j\omega T/2}\\ &=& 2\cos(\omega T/2)e^{-j\omega T/2} \end{eqnarray*}

It is now easy to see that

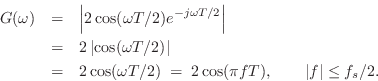
\begin{eqnarray*} G(\omega) &=& \left\vert 2\cos(\omega T/2)e^{-j\omega T/2}\rig... ... \eqsp 2\cos(\pi f T), \qquad \left\vert f\right\vert\leq f_s/2. \end{eqnarray*}

and

$\displaystyle \Theta(\omega) \eqsp -\frac{\omega T}{2} \eqsp -\pi f T \eqsp - \pi \frac{f}{f_s}, \qquad \left\vert f\right\vert\leq f_s/2. $

We have derived again the graph of Fig.1.7, which shows the complete frequency response of Eq.$ \,$(1.1). The gain of the simplest low-pass filter varies, as cosine varies, from 2 to 0 as the frequency of an input sinusoid goes from 0 to half the sampling rate. In other words, the amplitude response of Eq.$ \,$(1.1) goes sinusoidally from 2 to 0 as $ \omega T$ goes from 0 to $ \pi $. It does seem somewhat reasonable to consider it a low-pass, and it is a poor one in the sense that it is hard to see which frequency should be called the cut-off frequency. We see that the spectral ``roll-off'' is very slow, as low-pass filters go, and this is what we pay for the extreme simplicity of Eq.$ \,$(1.1). The phase response $ \Theta(\omega) = -\omega T/2$ is linear in frequency, which gives rise to a constant time delay irrespective of the signal frequency.

It deserves to be emphasized that all a linear time-invariant filter can do to a sinusoid is scale its amplitude and change its phase. Since a sinusoid is completely determined by its amplitude $ A$, frequency $ f$, and phase $ \phi$, the constraint on the filter is that the output must also be a sinusoid, and furthermore it must be at the same frequency as the input sinusoid. More explicitly:

$\textstyle \parbox{0.8\textwidth}{% If a sinusoid, $A_1\cos(\omega nT + \phi_1)... ...terized by its gain $A_2/A_1$, and phase $\phi_2 - \phi_1$, at each frequency.}$

Mathematically, a sinusoid has no beginning and no end, so there really are no start-up transients in the theoretical setting. However, in practice, we must approximate eternal sinusoids with finite-time sinusoids whose starting time was so long ago that the filter output is essentially the same as if the input had been applied forever.

Tying it all together, the general output of a linear time-invariant filter with a complex sinusoidal input may be expressed as

\begin{eqnarray*} y(n) &=& (\textit{Complex Filter Gain}) \;\textit{times}\;\, (... ...ith Radius $[G(\omega)A]$\ and Phase $[\phi + \Theta(\omega)]$}. \end{eqnarray*}

Summary

This chapter has introduced many of the concepts associated with digital filters, such as signal representations, filter representations, difference equations, signal flow graphs, software implementations, sine-wave analysis (real and complex), frequency response, amplitude response, phase response, and other related topics. We used a simple filter example to motivate the need for more advanced methods to analyze digital filters of arbitrary complexity. We found even in the simple example of Eq.$ \,$(1.1) that complex variables are much more compact and convenient for representing signals and analyzing filters than are trigonometric techniques. We employ a complex sinusoid $ A e^{j(\omega nT+\phi)}$ having three parameters: amplitude, phase, and frequency, and when we put a complex sinusoid into any linear time-invariant digital filter, the filter behaves as a simple complex gain $ H(e^{j\omega T})= G(\omega)e^{j\Theta(\omega)}$, where the magnitude $ G(\omega)$ and phase $ \Theta(\omega)$ are the amplitude response and phase response, respectively, of the filter.

Elementary Filter Theory Problems

See http://ccrma.stanford.edu/~jos/filtersp/Elementary_Filter_Theory_Problems.html.

Next Section:
Matlab Analysis of the Simplest Lowpass Filter
Previous Section:
Preface