Freeverb
A more recently developed Schroeder reverberator is ``Freeverb'' -- a public domain C++ program by ``Jezar at Dreampoint'' used extensively in the free-software world. It uses four Schroeder allpasses in series and eight parallel Schroeder-Moorer filtered-feedback comb-filters (§2.6.5) for each audio channel, and is said to be especially well tuned.
![\includegraphics[width=\twidth]{eps/freeverb}](http://www.dsprelated.com/josimages_new/pasp/img724.png) |
Figure 3.8 shows the default signal-processing settings for the Freeverb left stereo channel. Processing for the right channel is obtained by adding an integer to each of the twelve delay-line lengths. This integer is called stereospread, and its default value is 23. (See the file tuning.h for all constants and default values used by Freeverb.) Different software distributions may include slightly different default values in tuning.h. The values in Fig.3.8 were found in the ladspa-cmt-plugins package (``Computer Music Toolkit'') which is included in the Planet CCRMA distribution, and which is based on the June 2000 version of Freeverb, as of this writing. There are at least six more instances of Freeverb in the Planet CCRMA distribution alone.4.10
Freeverb Main Loop
The C++ code for the main processing loop of Freeverb is shown in Fig.3.9. Notice that it sums the two stereo input channels to create a mono signal that is fed to the reverberator, which then computes a stereo output signal.
void revmodel::processreplace(float *inputL, float *inputR,
float *outputL, float *outputR, long numsamples, int skip)
{
float outL,outR,input;
int i;
while(numsamples-- > 0)
{
outL = outR = 0;
input = (*inputL + *inputR) * gain;
// Accumulate comb filters in parallel
for(i=0; i<numcombs; i++) {
outL += combL[i].process(input);
outR += combR[i].process(input);
}
// Feed through allpasses in series
for(i=0; i<numallpasses; i++) {
outL = allpassL[i].process(outL);
outR = allpassR[i].process(outR);
}
// Calculate output REPLACING anything already there
*outputL = outL*wet1 + outR*wet2 + *inputL*dry;
*outputR = outR*wet1 + outL*wet2 + *inputR*dry;
// Increment sample pointers, allowing for interleave
// (if any)
inputL += skip; // For stereo buffers, skip = 2
inputR += skip;
outputL += skip;
outputR += skip;
}
}
|
From the code in Fig.3.9, we see that the left and right reverberator output channels outL and outR are combined with the left and right input channels inputL and inputR as follows:
![$\displaystyle \left[\begin{array}{c} \texttt{outputL} \\ [2pt] \texttt{outputR}...
...\left[\begin{array}{c} \texttt{outL} \\ [2pt] \texttt{outR} \end{array}\right]
$](http://www.dsprelated.com/josimages_new/pasp/img725.png)
Lowpass-Feedback Comb Filter
Inspection of comb.h in the Freeverb source shows that Freeverb's ``comb'' filter is more specifically a lowpass-feedback-comb filter (LBCF4.11--§2.6.5). It is constructed using a delay line whose output is lowpass-filtered and summed with the delay-line's input. The particular lowpass used in Freeverb is a unity-gain one-pole lowpass having the transfer function
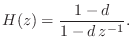
In Freeverb's comb section (comb.h and
comb.cpp), the ``damping'' ![]() is set initially to
is set initially to
Increasing the roomsize parameter (typically brought out to a
GUI slider) increases ![]() and hence the reverberation time. Since
and hence the reverberation time. Since
![]() is required for dc stability, the roomsize must be less
than 1.0714, and so the GUI slider max is typically 1 (
is required for dc stability, the roomsize must be less
than 1.0714, and so the GUI slider max is typically 1 (![]() ).
).
The feedback variable ![]() mainly determines reverberation
time at low-frequencies at which the feedback lowpass has negligible
effect. The feedback lowpass causes the reverberation time to
decrease with frequency, which is natural. At very high
frequencies--those for which the lowpass gain times
mainly determines reverberation
time at low-frequencies at which the feedback lowpass has negligible
effect. The feedback lowpass causes the reverberation time to
decrease with frequency, which is natural. At very high
frequencies--those for which the lowpass gain times ![]() is much less
than 0.5--the reverberation time becomes dominated by the diffusion
allpass filters (which have a fixed feedback coefficient of
is much less
than 0.5--the reverberation time becomes dominated by the diffusion
allpass filters (which have a fixed feedback coefficient of ![]() ).
Thus, in Freeverb, the ``room size'' parameter can be interpreted as
setting the low-frequency T60 (time to decay 60 dB), while the
``damping'' parameter controls how rapidly T60 shortens as a function
of increasing frequency. A lower-limit on T60 is given by the four
diffusion allpass filters.
).
Thus, in Freeverb, the ``room size'' parameter can be interpreted as
setting the low-frequency T60 (time to decay 60 dB), while the
``damping'' parameter controls how rapidly T60 shortens as a function
of increasing frequency. A lower-limit on T60 is given by the four
diffusion allpass filters.
In terms of the physical interpretation of the filtered-feedback comb-filter discussed in §2.6.5, Freeverb's roomsize parameter can be interpreted as the square-root of the low-frequency reflection-coefficient of each wall. That is, when a planewave bounces back and forth between two walls, the attenuation coefficient is roomsize after one round trip (two wall reflections). Therefore, a better name in this interpretation would be liveness or reflectivity. Since the round-trip delay is given in samples by the delay-line length, changing the roomsize requires changing the delay-line lengths in this interpretation.
Freeverb Allpass Approximation
In Eq.![]() (3.2) we defined the allpass notation
(3.2) we defined the allpass notation
![]() by
by
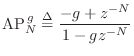

![\begin{eqnarray*}
\hbox{FBCF}_{N}^{\,g} &\isdef & \frac{1}{1 - g\,z^{-N}}\\ [5pt]
\hbox{FFCF}_{N}^{\,-1,1+g} &\isdef & -1 + (1+g)z^{-N}.
\end{eqnarray*}](http://www.dsprelated.com/josimages_new/pasp/img742.png)
A true allpass is obtained only for
![]() (reciprocal of the ``golden ratio''). The default value used in
Freeverb (see revmodel.cpp) is
(reciprocal of the ``golden ratio''). The default value used in
Freeverb (see revmodel.cpp) is ![]() . A detailed discussion
of feedforward and feedback comb filters appears
in §2.6, and corresponding Schroeder allpass filters are
described in §2.8.
. A detailed discussion
of feedforward and feedback comb filters appears
in §2.6, and corresponding Schroeder allpass filters are
described in §2.8.
Conclusions
Since Freeverb is a Schroeder-Moorer reverberator, and such reverbs have been around since the 1970s, its relatively recent success underscores the value of careful parameter tuning (typically by ear, but automatic optimizations are possible).
The idea of synthesizing right-channel processing from left-channel processing to obtain ``stereo spreading'' by enlarging all the delay lines by a fixed amount appears to have been introduced by Freeverb.
Next Section:
FDN Reverberation
Previous Section:
Schroeder Reverberators



















