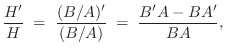Free Books
   Free Books    Introduction to Digital Filters  

Phase and Group Delay

In the previous sections we looked at the two most important frequency-domain representations for LTI digital filters, the transfer function $ H(z)$ and the frequency response:

$\displaystyle H(e^{j\omega T}) \isdefs \left.H(z)\right\vert _{z=e^{j\omega T}} $

We looked further at the polar form of the frequency response $ H(e^{j\omega T})= G(\omega)e^{j\Theta(\omega)}$, thereby breaking it down into the amplitude response $ G(\omega)$ times the phase-response term $ e^{j\Theta(\omega)}$.

In the next two sections we look at two alternative forms of the phase response: phase delay and group delay. After considering some examples and special cases, poles and zeros of the transfer function are discussed in the next chapter.

Phase Delay

The phase response $ \Theta(\omega)$ of an LTI filter gives the radian phase shift added to the phase of each sinusoidal component of the input signal. It is often more intuitive to consider instead the phase delay, defined as

$\displaystyle \zbox {P(\omega) \isdefs - \frac{\Theta(\omega)}{\omega}.} \qquad\hbox{(Phase Delay)} $

The phase delay gives the time delay in seconds experienced by each sinusoidal component of the input signal. For example, in the simplest lowpass filter of Chapter 1, we found that the phase response was $ \Theta(\omega) = -\omega T/2$, which corresponds to a phase delay $ P(\omega) = T/2$, or one-half sample. Thus, we can say precisely that the filter $ y(n) = x(n) + x(n - 1)$ exhibits half a sample of time delay at every frequency. (Regarding the discussion in §1.3.2, it is now obvious how we should define the filter phase response at frequencies 0 and $ f_s/2$.)

From a sinewave-analysis point of view, if the input to a filter with frequency response $ H(e^{j\omega T})= G(\omega)e^{j\Theta(\omega)}$ is

$\displaystyle x(n) = \cos(\omega nT) $

then the output is

\begin{eqnarray*} y(n) &=& G(\omega) \cos[\omega nT + \Theta(\omega)]\\ &=& G(\omega) \cos\{\omega[nT - P(\omega)]\} \end{eqnarray*}

and it can be clearly seen in this form that the phase delay expresses the phase response as a time delay in seconds.

Phase Unwrapping

In working with phase delay, it is often necessary to ``unwrap'' the phase response $ \Theta(\omega)$. Phase unwrapping ensures that all appropriate multiples of $ 2\pi$ have been included in $ \Theta(\omega)$. We defined $ \Theta(\omega)$ simply as the complex angle of the frequency response $ H(e^{j\omega T})$, and this is not sufficient for obtaining a phase response which can be converted to true time delay. If multiples of $ 2\pi$ are discarded, as is done in the definition of complex angle, the phase delay is modified by multiples of the sinusoidal period. Since LTI filter analysis is based on sinusoids without beginning or end, one cannot in principle distinguish between ``true'' phase delay and a phase delay with discarded sinusoidal periods when looking at a sinusoidal output at any given frequency. Nevertheless, it is often useful to define the filter phase response as a continuous function of frequency with the property that $ \Theta(0) = 0$ or $ \pi $ (for real filters). This specifies how to unwrap the phase response at all frequencies where the amplitude response is finite and nonzero. When the amplitude response goes to zero or infinity at some frequency, we can try to take a limit from below and above that frequency.

Matlab and Octave have a function called unwrap() which implements a numerical algorithm for phase unwrapping. Figures 7.6.2 and 7.6.2 show the effect of the unwrap function on the phase response of the example elliptic lowpass filter of §7.5.2, modified to contract the zeros from the unit circle to a circle of radius $ 0.95$ in the $ z$ plane: 

  [B,A] = ellip(4,1,20,0.5); % design lowpass filter
   B = B .* (0.95).^[1:length(B)]; % contract zeros by 0.95
  [H,w] = freqz(B,A);      % frequency response
  theta = angle(H);        % phase response
  thetauw = unwrap(theta); % unwrapped phase response
In Fig.7.6.2, the phase-response minimum has ``wrapped around'' to the top of the plot. In Fig.7.6.2, the phase response is continuous. We have contracted the zeros away from the unit circle in this example, because the phase response really does switch discontinuously by $ \pi $ radians when frequency passes through a point where the phases crosses zero along the unit circle (see Fig.7.3(b)). The unwrap function need not modify these discontinuities, but it is free to add or subtract any integer multiple of $ 2\pi$ in order to obtain the ``best looking'' discontinuity. Typically, for best results, such discontinuities should alternate between $ +\pi$ and $ -\pi$, making the phase response resemble a distorted ``square wave'', as in Fig.7.3(b). A more precise example appears in Fig.10.2.

Figure 7.4: Phase response of a modified order 4 elliptic function lowpass filter cutting off at $ f_s/4$.
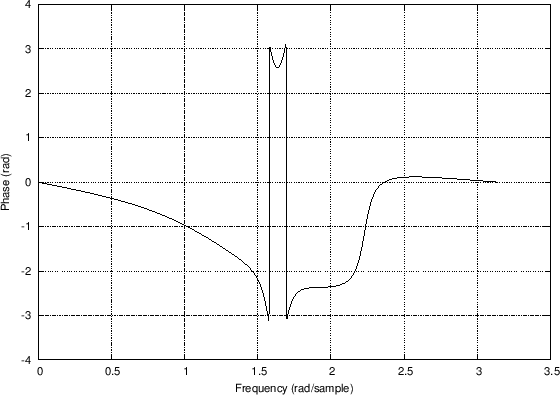
\includegraphics{eps/unwrapdemo1}
Phase Response

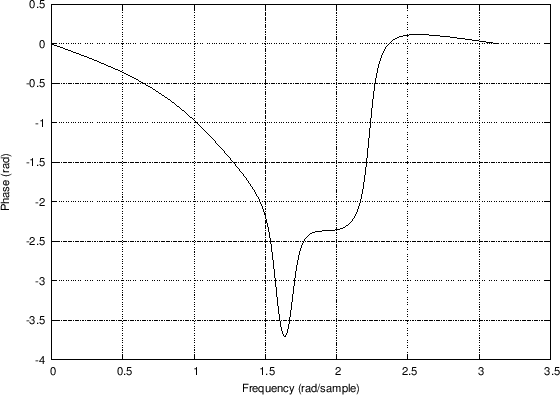
\includegraphics{eps/unwrapdemo2}
Unwrapped Response

Group Delay

A more commonly encountered representation of filter phase response is called the group delay, defined by

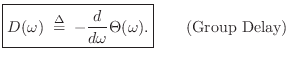
$\displaystyle \zbox {D(\omega) \isdefs - \frac{d}{d\omega} \Theta(\omega).} \qquad\hbox{(Group Delay)} $

For linear phase responses, i.e., $ \Theta(\omega) = -\alpha\omega$ for some constant $ \alpha$, the group delay and the phase delay are identical, and each may be interpreted as time delay (equal to $ \alpha$ samples when $ \omega\in[-\pi,\pi]$). If the phase response is nonlinear, then the relative phases of the sinusoidal signal components are generally altered by the filter. A nonlinear phase response normally causes a ``smearing'' of attack transients such as in percussive sounds. Another term for this type of phase distortion is phase dispersion. This can be seen below in §7.6.5.

An example of a linear phase response is that of the simplest lowpass filter, $ \Theta(\omega) = -\omega T/2 \,\,\Rightarrow\,\, P(\omega)=D(\omega)=T/2$. Thus, both the phase delay and the group delay of the simplest lowpass filter are equal to half a sample at every frequency.

For any reasonably smooth phase function, the group delay $ D(\omega)$ may be interpreted as the time delay of the amplitude envelope of a sinusoid at frequency $ \omega$ [63]. The bandwidth of the amplitude envelope in this interpretation must be restricted to a frequency interval over which the phase response is approximately linear. We derive this result in the next subsection.

Thus, the name ``group delay'' for $ D(\omega)$ refers to the fact that it specifies the delay experienced by a narrow-band ``group'' of sinusoidal components which have frequencies within a narrow frequency interval about $ \omega$. The width of this interval is limited to that over which $ D(\omega)$ is approximately constant.

Derivation of Group Delay as Modulation Delay

Suppose we write a narrowband signal centered at frequency $ \omega_c$ as

$\displaystyle x(n) = a_m(n) e^{j\omega_c n} \protect$ (8.6)

where $ \omega_c$ is defined as the carrier frequency (in radians per sample), and $ a_m(n)$ is some ``lowpass'' amplitude modulation signal. The modulation $ a_m$ can be complex-valued to represent either phase or amplitude modulation or both. By ``lowpass,'' we mean that the spectrum of $ a_m$ is concentrated near dc, i.e.,

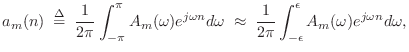
$\displaystyle a_m(n) \isdefs \frac{1}{2\pi} \int_{-\pi}^{\pi} A_m(\omega)e^{j\... ... \frac{1}{2\pi} \int_{-\epsilon}^{\epsilon} A_m(\omega)e^{j\omega n} d\omega, $

for some $ \left\vert\epsilon\right\vert\ll\pi$. The modulation bandwidth is thus bounded by $ 2\epsilon\ll\pi$.

Using the above frequency-domain expansion of $ a_m(n)$, $ x(n)$ can be written as

$\displaystyle x(n) \eqsp a_m(n) e^{j\omega_c n} \eqsp \left[\frac{1}{2\pi} \int_{-\epsilon}^{\epsilon} A_m(\omega)e^{j\omega n} d\omega\right] e^{j\omega_c n}, $

which we may view as a scaled superposition of sinusoidal components of the form

$\displaystyle x_\omega(n) \isdefs A_m(\omega)e^{j\omega n} e^{j\omega_c n} = A_m(\omega)e^{j(\omega+\omega_c) n} $

with $ \omega$ near 0. Let us now pass the frequency component $ x_\omega(n)$ through an LTI filter $ H(z)$ having frequency response

$\displaystyle H(e^{j\omega}) = G(\omega) e^{j\Theta(\omega)} $

to get

$\displaystyle y_\omega(n) = \left[G(\omega_c+\omega)A_m(\omega)\right] e^{j[(\omega_c +\omega) n + \Theta(\omega_c+\omega)]}. \protect$ (8.7)

Assuming the phase response $ \Theta(\omega)$ is approximately linear over the narrow frequency interval $ \omega\in[\omega_c-\epsilon,\omega_c+\epsilon]$, we can write

$\displaystyle \Theta(\omega_c+\omega)\;\approx\; \Theta(\omega_c) + \Theta^\prime(\omega_c)\omega \isdefs \Theta(\omega_c) - D(\omega_c)\omega, $

where $ D(\omega_c)$ is the filter group delay at $ \omega_c$. Making this substitution in Eq.$ \,$(7.7) gives

\begin{eqnarray*} y_\omega(n) &=& \left[G(\omega_c+\omega)A_m(\omega)\right] e^... ...\right] e^{j\omega[n-D(\omega_c)]} e^{j\omega_c[n-P(\omega_c)]}, \end{eqnarray*}

where we also used the definition of phase delay, $ P(\omega_c) = -\Theta(\omega_c)/\omega_c$, in the last step. In this expression we can already see that the carrier sinusoid is delayed by the phase delay, while the amplitude-envelope frequency-component is delayed by the group delay. Integrating over $ \omega$ to recombine the sinusoidal components (i.e., using a Fourier superposition integral for $ y$) gives

\begin{eqnarray*} y(n) &=& \frac{1}{2\pi}\int_{\omega} y_\omega(n) d\omega \\ &... ...)]}\\ &=& a^f[n-D(\omega_c)] \cdot e^{j\omega_c[n-P(\omega_c)]} \end{eqnarray*}

where $ a^f(n)$ denotes a zero-phase filtering of the amplitude envelope $ a(n)$ by $ G(\omega+\omega_c)$. We see that the amplitude modulation is delayed by $ D(\omega_c)$ while the carrier wave is delayed by $ P(\omega_c)$.

We have shown that, for narrowband signals expressed as in Eq.$ \,$(7.6) as a modulation envelope times a sinusoidal carrier, the carrier wave is delayed by the filter phase delay, while the modulation is delayed by the filter group delay, provided that the filter phase response is approximately linear over the narrowband frequency interval.

Group Delay Examples in Matlab

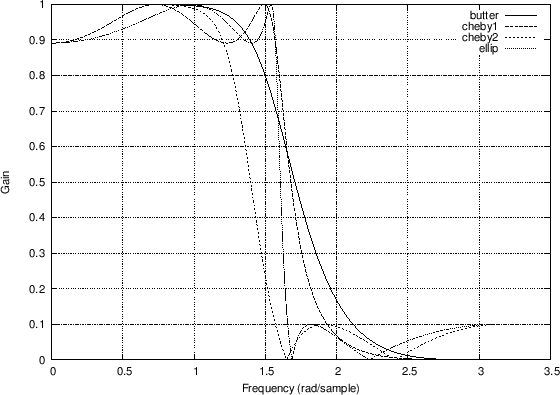
Figure 7.6 compares the group delay responses for a number of classic lowpass filters, including the example of Fig.7.2. The matlab code is listed in Fig.7.5. See, e.g., Parks and Burrus [64] for a discussion of Butterworth, Chebyshev, and Elliptic Function digital filter design. See also §I.2 for details on the Butterworth case. The various types may be summarized as follows:

  • Butterworth filters are maximally flat in middle of the passband.
  • Chebyshev Type I filters are ``equiripple'' in the passband and ``Butterworth'' in the stopband.
  • Chebyshev Type II filters are ``Butterworth'' in the passband and equiripple in the stopband.
  • Elliptic function filters are equiripple in both the passband and stopband.
Here, ``equiripple'' means ``equal ripple''; that is, the error oscillates with equal peak magnitudes across the band. An equiripple error characterizes optimality in the Chebyshev sense [64,78].

As Fig.7.6.4 indicates, and as is well known, the Butterworth filter has the flattest group delay curve (and most gentle transition from passband to stopband) for the four types compared. The elliptic function filter has the largest amount of ``delay distortion'' near the cut-off frequency (passband edge frequency). Fundamentally, the more abrupt the transition from passband to stopband, the greater the delay-distortion across that transition, for any minimum-phase filter. (Minimum-phase filters are introduced in Chapter 11.) The delay-distortion can be compensated by delay equalization, i.e., adding delay at other frequencies in order approach an overall constant group delay versus frequency. Delay equalization is typically carried out using an allpass filter (defined in §B.2) in series with the filter to be delay-equalized [1].

Figure 7.5: Program (matlab) for comparing the amplitude and group-delay responses of four classic lowpass filter types: Butterworth, Chebyshev Type I, Chebyshev Type II, and Elliptic Function.
  
[Bb,Ab] = butter(4,0.5); % order 4, cutoff at 0.5 * pi
Hb=freqz(Bb,Ab);
Db=grpdelay(Bb,Ab);

[Bc1,Ac1] = cheby1(4,1,0.5); % 1 dB passband ripple
Hc1=freqz(Bc1,Ac1);
Dc1=grpdelay(Bc1,Ac1);

[Bc2,Ac2] = cheby2(4,20,0.5); % 20 dB stopband attenuation
Hc2=freqz(Bc2,Ac2);
Dc2=grpdelay(Bc2,Ac2);

[Be,Ae] = ellip(4,1,20,0.5);  % like cheby1 + cheby2
He=freqz(Be,Ae);
[De,w]=grpdelay(Be,Ae);

figure(1); plot(w,abs([Hb,Hc1,Hc2,He])); grid('on');
xlabel('Frequency (rad/sample)'); ylabel('Gain');
legend('butter','cheby1','cheby2','ellip');
saveplot('../eps/grpdelaydemo1.eps');

figure(2); plot(w,[Db,Dc1,Dc2,De]); grid('on');
xlabel('Frequency (rad/sample)'); ylabel('Delay (samples)');
legend('butter','cheby1','cheby2','ellip');
saveplot('../eps/grpdelaydemo2.eps');

Figure 7.6: Comparison of amplitude and group-delay responses for classic lowpass-filter types Butterworth, Chebyshev Type I, Chebyshev Type II, and Elliptic Function. Plots generated by Octave 2.9.7 and octave-forge 2006-07-09.
\includegraphics{eps/grpdelaydemo1}

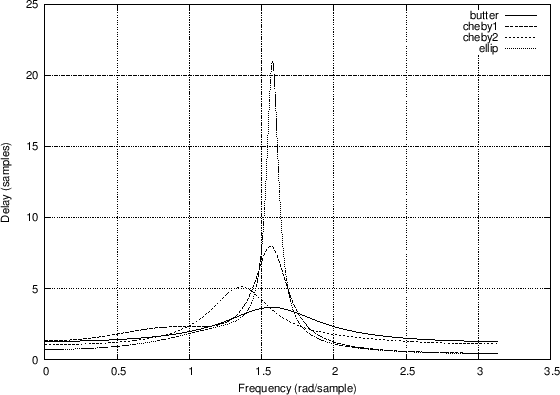
\includegraphics{eps/grpdelaydemo2}
Group Delays

Vocoder Analysis

The definitions of phase delay and group delay apply quite naturally to the analysis of the vocoder (``voice coder'') [21,26,54,76]. The vocoder provides a bank of bandpass filters which decompose the input signal into narrow spectral ``slices.'' This is the analysis step. For synthesis (often called additive synthesis), a bank of sinusoidal oscillators is provided, having amplitude and frequency control inputs. The oscillator frequencies are tuned to the filter center frequencies, and the amplitude controls are driven by the amplitude envelopes measured in the filter-bank analysis. (Typically, some data reduction or envelope modification has taken place in the amplitude envelope set.) With these oscillators, the band slices are independently regenerated and summed together to resynthesize the signal.

Suppose we excite only channel $ k$ of the vocoder with the input signal

$\displaystyle a(nT) \cos(\omega_knT), \qquad n=0,1,2,\ldots $

where $ \omega_k$ is the center frequency of the channel in radians per second, $ T$ is the sampling interval in seconds, and the bandwidth of $ a(nT)$ is smaller than the channel bandwidth. We may regard this input signal as an amplitude modulated sinusoid. The component $ \cos(\omega_k n T)$ can be called the carrier wave, while $ a(nT)\geq 0$ is the amplitude envelope.

If the phase of each channel filter is linear in frequency within the passband (or at least across the width of the spectrum $ A(e^{j\omega T})$ of $ a(nT)$), and if each channel filter has a flat amplitude response in its passband, then the filter output will be, by the analysis of the previous section,

$\displaystyle y_k(n) \;\approx\; a[nT - D(\omega_k)] \cos\{\omega_k[nT - P(\omega_k)]\} \protect$ (8.8)

where $ P(\omega_k)$ is the phase delay of the channel filter at frequency $ \omega_k$, and $ D(\omega_k)$ is the group delay at that frequency. Thus, in vocoder analysis for additive synthesis, the phase delay of the analysis filter bank gives the time delay experienced by the oscillator carrier waves, while the group delay of the analysis filter bank gives the time delay imposed on the estimated oscillator amplitude-envelope functions.

Note that a nonlinear phase response generally results in $ D(\omega_k)\neq P(\omega_k)$, and $ D(\omega_k)\neq D(\omega_l)$ for $ k\neq l$. As a result, the dispersive nature of additive synthesis reconstruction in this case can be seen in Eq.$ \,$(7.8).

Numerical Computation of Group Delay

The definition of group delay,

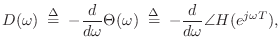
$\displaystyle D(\omega) \isdefs - \frac{d}{d\omega} \Theta(\omega) \isdefs - \frac{d}{d\omega} \angle H(e^{j\omega T}), $

does not give an immediately useful recipe for computing group delay numerically. In this section, we describe the theory of operation behind the matlab function for group-delay computation given in §J.8.

A more useful form of the group delay arises from the logarithmic derivative of the frequency response. Expressing the frequency response $ H(e^{j\omega T})$ in polar form as

$\displaystyle H(e^{j\omega T}) \isdefs G(\omega)e^{j\Theta(\omega)} $

yields the following logarithmic decomposition of magnitude and phase:

$\displaystyle \ln H(e^{j\omega T}) = \ln G(\omega) + j\Theta(\omega) $

Thus, the real part of the logarithm of the frequency response equals the log amplitude response, while the imaginary part equals the phase response.

Since differentiation is linear, the logarithmic derivative becomes

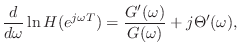
$\displaystyle \frac{d}{d\omega} \ln H(e^{j\omega T}) = \frac{G^\prime(\omega)}{G(\omega)} + j\Theta^\prime(\omega), $

where $ G^\prime(\omega)$ and $ \Theta^\prime(\omega)$ denote the derivatives of $ G(\omega)$ and $ \Theta(\omega)$, respectively, with respect to $ \omega$. We may therefore express the group delay as

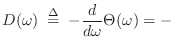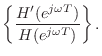
$\displaystyle D(\omega) \isdefs - \frac{d}{d\omega} \Theta(\omega) = -$im$\displaystyle \left\{\frac{d}{d\omega} \ln H(e^{j\omega T})\right\} = -$im$\displaystyle \left\{\frac{H^\prime(e^{j\omega T})}{H(e^{j\omega T})}\right\}. $

Consider first the FIR case in which $ H(z)=B(z)$, with

$\displaystyle B(z) \isdefs b_0 + b_1z^{-1}+ b_2z^{-2}+ \cdots + b_M z^{-M}. \protect$ (8.9)

In this case, the derivative is simply

\begin{eqnarray*} B^\prime(e^{j\omega T}) &\isdef & \frac{d}{d\omega}\left[b_0 ... ...b_M e^{-jM\omega T}\right]\\ &\isdef & -jT\,B_r(e^{j\omega T}), \end{eqnarray*}

where $ B_r(z)$ denotes ``$ B$ ramped'', i.e., the $ i$th coefficient of the polynomial $ B_r$ is $ i\,b_i$, for $ i=0,1,2,\ldots,M$. In matlab, we may compute Br from B via the following statement:

Br = B .* [0:M]; % Compute ramped B polynomial
The group delay of an FIR filter $ B(z)$ can now be written as

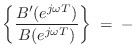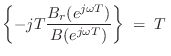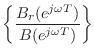
$\displaystyle D(\omega) \eqsp -$im$\displaystyle \left\{\frac{B^\prime(e^{j\omega T})}{B(e^{j\omega T})}\right\} \eqsp -$im$\displaystyle \left\{-jT\frac{B_r(e^{j\omega T})}{B(e^{j\omega T})}\right\} \eqsp T\,$re$\displaystyle \left\{\frac{B_r(e^{j\omega T})}{B(e^{j\omega T})}\right\} $

In matlab, the group delay, in samples, can be computed simply as
D = real(fft(Br) ./ fft(B))
where the fft, of course, approximates the Discrete Time Fourier Transform (DTFT). Such sampling of the frequency axis by this approximation is information-preserving whenever the number of samples (FFT length) exceeds the polynomial order $ M$. The ratio of sampled DTFTs, however, is undersampled, in general. In fact, we may have $ B(e^{j\omega T})=0$ at some frequencies (``zeros on the unit circle''). The grpdelay matlab utility in §J.8 watches out for division by zero, and simply sets the group delay to zero at such frequencies. Note that the true group delay approaches infinite magnitude as either a zero or pole approaches the unit circle.

Finally, when there are both poles and zeros, we have

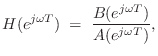
$\displaystyle H(e^{j\omega T}) \eqsp \frac{B(e^{j\omega T})}{A(e^{j\omega T})}, $

where $ B(e^{j\omega T})$ is given in Eq.$ \,$(7.9), and

$\displaystyle A(z) \isdefs 1 + a_1z^{-1}+ a_2z^{-2}+ \cdots + a_N z^{-N}. \protect$ (8.10)

Straightforward differentiation yields

$\displaystyle \frac{H^\prime}{H} \eqsp \frac{(B/A)^\prime}{(B/A)} \eqsp \frac{B^\prime A - B A^\prime}{BA}, \protect$ (8.11)

and this can be implemented analogous to the FIR case discussed above. However, a faster algorithm (usually) results from converting the IIR case to the FIR case:

$\displaystyle C(z) \isdefs B(z)\left[ z^{-N}\overline{A}(1/z)\right] \isdefs B(z)\tilde{A}(z) \protect$ (8.12)

where

$\displaystyle \tilde{A}(z)\isdefs z^{-N}\overline{A}(1/z) \eqsp [\overline{a}_... ..._{N-1}z^{-1},\overline{a}_{N-2}z^{-2},\ldots,\overline{a}_1 z^{-(N-1)}+z^{-N}] $

may be called the ``flip-conjugate'' or ``Hermitian conjugate'' of the polynomial $ A(z)$.8.4In matlab, the C polynomial is given by
C = conv(B,fliplr(conj(A)));
It is straightforward to show (Problem 11) that

$\displaystyle \angle\tilde{A}(e^{j\omega T}) \eqsp -\angle A(e^{j\omega T}) - N\omega T. $

The phase of the IIR filter $ H(z)=B(z)/A(z)$ is therefore

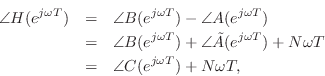
\begin{eqnarray*} \angle H(e^{j\omega T}) &=& \angle B(e^{j\omega T}) - \angle ... ...mega T}) + N\omega T\\ &=& \angle C(e^{j\omega T}) + N\omega T, \end{eqnarray*}

and the group delay computation thus reduces to the FIR case:

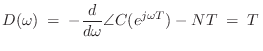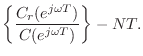
$\displaystyle D(\omega) \eqsp - \frac{d}{d\omega} \angle C(e^{j\omega T}) - NT \eqsp T\,$re$\displaystyle \left\{\frac{C_r(e^{j\omega T})}{C(e^{j\omega T})}\right\} - NT. $

This method is implemented in §J.8.

Next Section:
Frequency Response Analysis Problems
Previous Section:
Frequency Response as a Ratio of DTFTs