An Efficient Linear Interpolation Scheme
This article presents a computationally-efficient linear interpolation trick that requires at most one multiply per output sample.
Simplest Calculation of Half-band Filter Coefficients
Half-band filters are lowpass FIR filters with cut-off frequency of one-quarter of sampling frequency fs and odd symmetry about fs/4 [1]*. And it so happens that almost half of the coefficients are zero. The passband and stopband bandwiths are equal, making these filters useful for decimation-by-2 and interpolation-by-2. Since the zero coefficients make them computationally efficient, these filters are ubiquitous in DSP systems. Here we will compute half-band coefficients using the window method. While the window method typically does not yield the fewest taps for a given performance, it is useful for learning about half-band filters. Efficient equiripple half-band filters can be designed using the Matlab function firhalfband [2].
Errata for the book: 'Understanding Digital Signal Processing'
Errata 3rd Ed. International Version.pdfErrata 3rd Ed. International Version.pdfThis blog post provides, in one place, the errata for each of the many different Editions/Printings of my book Understanding Digital Signal Processing. If you...
Feedback Controllers - Making Hardware with Firmware. Part I. Introduction
Introduction to the topic This is the 1st in a series of articles looking at how we can use DSP and Feedback Control Sciences along with some mixed-signal electronics and number-crunching capability (e.g. FPGA), to create arbitrary...
How to Find a Fast Floating-Point atan2 Approximation
Context Over a short period of time, I came across nearly identical approximations of the two parameter arctangent function, atan2, developed by different companies, in different countries, and even in different decades. Fascinated...
A Beginner's Guide to OFDM
In the recent past, high data rate wireless communications is often considered synonymous to an Orthogonal Frequency Division Multiplexing (OFDM) system. OFDM is a special case of multi-carrier communication as opposed to a conventional...
Sinusoidal Frequency Estimation Based on Time-Domain Samples
The topic of estimating a noise-free real or complex sinusoid's frequency, based on fast Fourier transform (FFT) samples, has been presented in recent blogs here on dsprelated.com. For completeness, it's worth knowing that simple frequency estimation algorithms exist that do not require FFTs to be performed . Below I present three frequency estimation algorithms that use time-domain samples, and illustrate a very important principle regarding so called "exact" mathematically-derived DSP algorithms.
Launch of Youtube Channel: My First Videos - Embedded World 2017
I went to Embedded World 2017 in Nuremberg with an ambitious plan; I would make video highlights of several exhibits (booths) to be presented to the *Related sites audience. I would try to make the vendors focus their pitch on the essential...
A Two Bin Exact Frequency Formula for a Pure Complex Tone in a DFT
Introduction This is an article to hopefully give a better understanding to the Discrete Fourier Transform (DFT) by deriving an exact formula for the frequency of a complex tone in a DFT. It is basically a parallel treatment to the real case...
DFT Bin Value Formulas for Pure Complex Tones
Introduction This is an article to hopefully give a better understanding to the Discrete Fourier Transform (DFT) by deriving an analytical formula for the DFT of pure complex tones and an alternative variation. It is basically a parallel...
Third-Order Distortion of a Digitally-Modulated Signal
Analog designers are always harping about amplifier third-order distortion. Why? In this article, we'll look at why third-order distortion is important, and simulate a QAM signal with third order distortion.
A Brief Introduction To Romberg Integration
This article briefly describes a remarkable integration algorithm, called "Romberg integration." The algorithm is used in the field of numerical analysis but it's not so well-known in the world of DSP.
Sinusoidal Frequency Estimation Based on Time-Domain Samples
The topic of estimating a noise-free real or complex sinusoid's frequency, based on fast Fourier transform (FFT) samples, has been presented in recent blogs here on dsprelated.com. For completeness, it's worth knowing that simple frequency estimation algorithms exist that do not require FFTs to be performed . Below I present three frequency estimation algorithms that use time-domain samples, and illustrate a very important principle regarding so called "exact" mathematically-derived DSP algorithms.
Round Round Get Around: Why Fixed-Point Right-Shifts Are Just Fine
Today’s topic is rounding in embedded systems, or more specifically, why you don’t need to worry about it in many cases.One of the issues faced in computer arithmetic is that exact arithmetic requires an ever-increasing bit length to...
Wavelets II - Vanishing Moments and Spectral Factorization
In the previous blog post I described the workings of the Fast Wavelet Transform (FWT) and how wavelets and filters are related. As promised, in this article we will see how to construct useful filters. Concretely, we will find a way to calculate...
Discrete Wavelet Transform Filter Bank Implementation (part 1)
UPDATE: Added graphs and code to explain the frequency division of the branches The focus of this article is to briefly explain an implementation of this transform and several filter bank forms. Theoretical information about DWT can be found...
3 Good News
Good News #1 Last week, I announced a new and ambitious reward program that will be funded by the new Vendors Directory. This week, I am happy to announce that we have our firsts two sponsors! Quantum Leaps & Abelon Systems have...
An s-Plane to z-Plane Mapping Example
While surfing around the Internet recently I encountered the 's-plane to z-plane mapping' diagram shown in Figure 1. At first I thought the diagram was neat because it's a good example of the old English idiom: "A picture is worth a thousand...
Coupled-Form 2nd-Order IIR Resonators: A Contradiction Resolved
This blog clarifies how to obtain and interpret the z-domain transfer function of the coupled-form 2nd-order IIR resonator. The coupled-form 2nd-order IIR resonator was developed to overcome a shortcoming in the standard 2nd-order IIR resonator....
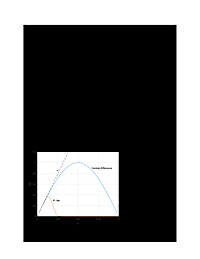
Evaluate Noise Performance of Discrete-Time Differentiators
When it comes to noise, all differentiators are not created equal. Figure 1 shows the magnitude response of two differentiators. They both have a useful bandwidth of a little less than π/8 radians (based on maximum magnitude response...
