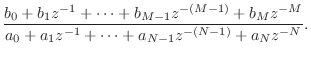Matlab Utilities

This appendix provides software listings for various analysis utilities written in matlab. Except for plot-related commands, they should be compatible either Matlab or Octave.

Time Plots: myplot.m

function myplot(x, y, sym, ttl, xlab, ylab, grd, lgnd)
% MYPLOT - Generic plot - compatibility wrapper for plot()
%          Octave version.  See below for Matlab version.
%          In Octave, title and axis labels must be issued
%          BEFORE the plot() command.

  if nargin<8, lgnd=''; end
  if nargin<7, grd=1; end
  if nargin<6, ylab=''; end
  if nargin<5, xlab=''; end
  if nargin<4, ttl=''; end
  if nargin<3, sym='*k'; end
  if nargin<2, y=x; x=0:length(y)-1; end

  title(ttl);
  ylabel(ylab);
  xlabel(xlab);
  if grd, grid('on'); else grid('off'); end
  plot(x,y,sym);
  legend(lgnd);

function myplot(x, y, sym, ttl, xlab, ylab, grd, lgnd)
% MYPLOT - Generic plot - compatibility wrapper for plot()
%          Matlab version. Title and axis labels must be
%          placed AFTER the plot() command.

  if nargin<8, lgnd=''; end
  if nargin<7, grd=1; end
  if nargin<6, ylab=''; end
  if nargin<5, xlab=''; end
  if nargin<4, ttl=''; end
  if nargin<3, sym='*k'; end
  if nargin<2, y=x; x=0:length(y)-1; end

  plot(x,y,sym);
  title(ttl);
  ylabel(ylab);
  xlabel(xlab);
  if grd, grid('on'); end
  legend(lgnd);

Frequency Plots: freqplot.m

function freqplot(fdata, ydata, symbol, ttl, xlab, ylab)
% FREQPLOT - Plot a function of frequency:
%
%   freqplot(fdata[,ydata[,symbol[,title[,xlab[,ylab]]]]])
%
%   This version is most compatible with Octave.
%   In Matlab, the title and axis labels may be lost.
%   For Matlab compatibility, move the plot() command
%   before title() and axis label commands.

  if nargin<6, ylab=''; end
  if nargin<5, xlab='Frequency'; end
  if nargin<4, ttl=''; end
  if nargin<3, symbol=''; end
  if nargin<2, ydata=fdata; fdata=0:length(ydata)-1; end

  if ttl, title(ttl); end
  if length(ylab)>0, ylabel(ylab); end
  if length(xlab)>0, xlabel(xlab); end
  grid('on');
  plot(fdata,ydata,symbol);

function freqplot(fdata, ydata, symbol, ttl, xlab, ylab)
% FREQPLOT - Plot a function of time, Matlab version.

  if nargin<6, ylab=''; end
  if nargin<5, xlab='Frequency (Hz)'; end
  if nargin<4, ttl=''; end
  if nargin<3, symbol=''; end
  if nargin<2, fdata=0:length(ydata)-1; end

  plot(fdata,ydata,symbol); grid;
  if ttl, title(ttl); end
  if ylab, ylabel(ylab); end
  xlabel(xlab);

Saving Plots to Disk: saveplot.m

function saveplot(filename,optargs)
% SAVEPLOT - Save current plot to disk in a PostScript file.
%            This version is compatible only with Octave.
%            In Matlab, just say 'print -deps[c] filename'.
%            *** MULTIPLOT MODE NOT SUPPORTED ***
%            (only get last plot)

if (nargin<2), optargs = ''; end;
% optargs to consider:
%   landscape
%   color
%   solid
%   "<fontname>" <fontsize>
%   lw <width> [default = 1.0]

gset terminal push

gset nomultiplot % can't set out terminal in multiplot mode
%gset terminal fig % in this output format, you can edit it!
cmd=['gset terminal postscript eps monochrome enhanced',...
     optargs];
eval(cmd);

disp(sprintf('Writing current plot to %s',filename));
cmd = sprintf('gset output \'%s\';',filename); eval(cmd);

replot
% remultiplot -- does not yet exist in gnuplot
closeplot

gset terminal pop

function saveplot(filename)
% SAVEPLOT - Save current plot to disk in a PostScript file.
%            This version is compatible only with Matlab.

cmd = ['print -deps ',filename]; % for color, use '-depsc'
disp(cmd); eval(cmd);

Frequency Response Plots: plotfr.m

Figure J.7 lists a Matlab function for plotting frequency-response magnitude and phase. (See also Fig.7.1.) Since Octave does not yet support saving multiple ``subplots'' to disk for later printing, we do not have an Octave-compatible version here. At present, Matlab's graphics support is much more extensive and robust than that in Octave's (which is based on a shaky and Matlab-incompatible interface to gnuplot). Another free alternative to consider for making nice Matlab-style 2D plots is matplotlib.

function [plothandle] = plotfr(X,f);
% PLOTFR - Plot frequency-response magnitude & phase.
%          Requires Mathworks Matlab.
%
% X = frequency response
% f = vector of corresponding frequency values

Xm = abs(X);         % Amplitude response
Xmdb = 20*log10(Xm); % Prefer dB for audio work
Xp = angle(X);       % Phase response

if nargin<2, N=length(X); f=(0:N-1)/(2*(N-1)); end
subplot(2,1,1);
plot(f,Xmdb,'-k'); grid;
ylabel('Gain (dB)');
xlabel('Normalized Frequency (cycles/sample)');
axis tight;
text(-0.07,max(Xmdb),'(a)');

subplot(2,1,2);
plot(f,Xp,'-k'); grid;
ylabel('Phase Shift (radians)');
xlabel('Normalized Frequency (cycles/sample)');
axis tight;
text(-0.07,max(Xp),'(b)');

if exist('OCTAVE_VERSION')
  plothandle = 0; % gcf undefined in Octave
else
  plothandle = gcf;
end

Partial Fraction Expansion: residuez.m

Figure J.8 gives a listing of a matlab function for computing a ``left-justified'' partial fraction expansion (PFE) of an IIR digital filter as described in §6.8 (and below). This function, along with its ``right justified'' counterpart, residued, are included in the octave-forge matlab library for Octave.^J.1

function [r, p, f, m] = residuez(B, A, tol)
if nargin<3, tol=0.001; end
NUM = B(:)'; DEN = A(:)';
% Matlab's residue does not return m (implied by p):
[r,p,f,m]=residue(conj(fliplr(NUM)),conj(fliplr(DEN)),tol);
p = 1 ./ p;
r = r .* ((-p) .^m);
if f, f = conj(fliplr(f)); end

This code was written for Octave, but it also runs in Matlab if the 'm' outputs (pole multiplicity counts) are omitted (two places). The input arguments are compatible with the existing residuez function in the Matlab Signal Processing Toolbox.

Method

As can be seen from the code listing, this implementation of residuez simply calls residue, which was written to carry out the partial fraction expansions of -plane (continuous-time) transfer functions :

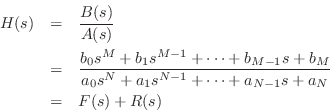
where is the ``quotient'' and is the ``remainder'' in the PFE:

			(J.1)

In the discrete-time case, we have the -plane transfer function

			(J.2)

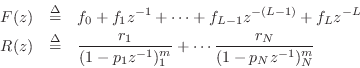
where .

We see that the -plane case formally does what we desire if we treat -plane polynomials as polynomials in instead of . From Eq.(J.2), we see that this requires reversing the coefficient-order of B and A in the call to residue. In the returned result, we obtain terms such as

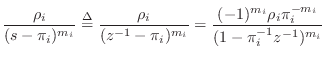
Example with Repeated Poles

The following Matlab code performs a partial fraction expansion of a filter having three pairs of repeated roots (one real and two complex):^J.2

N = 1000;  % number of time samples to compute
A = [ 1 0 0 1 0 0 0.25];
B = [ 1 0 0 0 0 0 0];

% Compute "trusted" impulse response:
h_tdl = filter(B, A, [1 zeros(1, N-1)]);

% Compute partial fraction expansion (PFE):
[R,P,K] = residuez(B, A);

% PFE impulse response:
n = [0:N-1];
h_pfe = zeros(1,N);
for i = 1:size(R)
  % repeated roots are not detected exactly:
  if i>1 && abs(P(i)-P(i-1))<1E-7
    h_pfe = h_pfe + (R(i) * (n+1) .* P(i).^n);
    disp(sprintf('Pole %d is a repeat of pole %d',i,i-1));
    % if i>2 && abs(P(i)-P(i-2))<1E-7 ...
  else
    h_pfe = h_pfe + (R(i) * P(i).^n);
  end
end

err = abs(max(h_pfe-h_tdl)) % should be about 5E-8

Partial Fraction Expansion: residued.m

Figure J.9 gives a listing of a matlab function for computing a ``right justified'' partial fraction expansion (PFE) of an IIR digital filter as described in §6.8 (and below).

The code in Fig.J.9 was written to work in Octave, and also in Matlab if the 'm' argument is omitted (in two places).

function [r, p, f, e] = residued(b, a, toler)
if nargin<3, toler=0.001; end
NUM = b(:)';
DEN = a(:)';
nb = length(NUM);
na = length(DEN);
f = [];
if na<=nb
  f = filter(NUM,DEN,[1,zeros(nb-na)]);
  NUM = NUM - conv(DEN,f);
  NUM = NUM(nb-na+2:end);
end
[r,p,f2,e] = residuez(NUM,DEN,toler);

Method

The FIR part is first extracted, and the (strictly proper) remainder is passed to residuez for expansion of the IIR part (into a sum of complex resonators). One must remember that, in this case, the impulse-response of the IIR part begins after the impulse-response of the FIR part has finished, i.e.,

See §6.8.8 for an example usage of residued (with a comparison to residuez).

Parallel SOS to Transfer Function: psos2tf.m

Figure J.10 lists a matlab function for computing the direct-form transfer-function polynomials from parallel second-order section coefficients. This is in contrast to the existing function sos2tf which converts series second-order sections to transfer-function form.

function [B,A] = psos2tf(sos,g)

if nargin<2, g=1; end

[nsecs,tmp] = size(sos);
if nsecs<1, B=[]; A=[]; return; end
Bs = sos(:,1:3);
As = sos(:,4:6);
B = Bs(1,:);
A = As(1,:);
for i=2:nsecs
  B = conv(B,As(i,:)) + conv(A,Bs(i,:));
  A = conv(A,As(i,:));
end

Group Delay Computation: grpdelay.m

Figure J.11 gives a listing of a matlab program for computing the group delay of an IIR digital filter using the method described in §7.6.6.

In Matlab with the Signal Processing Toolbox installed, (or Octave with the Octave Forge package installed), say 'help grpdelay' for usage documentation, and say 'type grpdelay' to additionally see test, demo, and plotting code. Here, we include only the code relevant to computation of the group delay itself.

function [gd,w] = grpdelay(b,a,nfft,whole,Fs)

  if (nargin<1 || nargin>5)
    usage("[g,w]=grpdelay(b [, a [, n [,'whole'[,Fs]]]])");
  end
  if nargin<5
    Fs=0; % return w in radians per sample
    if nargin<4, whole='';
    elseif ~isstr(whole)
      Fs = whole;
      whole = '';
    end
    if nargin<3, nfft=512; end
    if nargin<2, a=1; end
  end

  if strcmp(whole,'whole')==0, nfft = 2*nfft; end

  w = 2*pi*[0:nfft-1]/nfft;
  if Fs>0, w = Fs*w/(2*pi); end

  oa = length(a)-1;             % order of a(z)
  oc = oa + length(b)-1;        % order of c(z)
  c = conv(b,fliplr(a));	% c(z) = b(z)*a(1/z)*z^(-oa)
  cr = c.*[0:oc];               % derivative of c wrt 1/z
  num = fft(cr,nfft);
  den = fft(c,nfft);
  minmag = 10*eps;
  polebins = find(abs(den)<minmag);
  for b=polebins
    disp('*** grpdelay: group delay singular! setting to 0')
    num(b) = 0;
    den(b) = 1;
  end
  gd = real(num ./ den) - oa;

  if strcmp(whole,'whole')==0
    ns = nfft/2; % Matlab convention - should be nfft/2 + 1
    gd = gd(1:ns);
    w = w(1:ns);
  end

  w = w'; % Matlab returns column vectors
  gd = gd';

Matlab listing: fold.m

The fold() function ``time-aliases'' the noncausal part of a function onto its causal part. When applied to the inverse Fourier transform of a log-spectrum, it converts non-minimum-phase zeros to minimum-phase zeros. (See §J.11 for an example usage.)

function [rw] = fold(r)
% [rw] = fold(r)
% Fold left wing of vector in "FFT buffer format"
% onto right wing
% J.O. Smith, 1982-2002

   [m,n] = size(r);
   if m*n ~= m+n-1
     error('fold.m: input must be a vector');
   end
   flipped = 0;
   if (m > n)
     n = m;
     r = r.';
     flipped = 1;
   end
   if n < 3, rw = r; return;
   elseif mod(n,2)==1,
       nt = (n+1)/2;
       rw = [ r(1), r(2:nt) + conj(r(n:-1:nt+1)), ...
             0*ones(1,n-nt) ];
   else
       nt = n/2;
       rf = [r(2:nt),0];
       rf = rf + conj(r(n:-1:nt+1));
       rw = [ r(1) , rf , 0*ones(1,n-nt-1) ];
   end;

   if flipped
     rw = rw.';
   end

Matlab listing: clipdb.m

The clipdb() function prevents the log magnitude of a signal from being too large and negative. (See §J.11 for an example usage.)

function [clipped] = clipdb(s,cutoff)
% [clipped] = clipdb(s,cutoff)
% Clip magnitude of s at its maximum + cutoff in dB.
% Example: clip(s,-100) makes sure the minimum magnitude
% of s is not more than 100dB below its maximum magnitude.
% If s is zero, nothing is done.

clipped = s;
as = abs(s);
mas = max(as(:));
if mas==0, return; end
if cutoff >= 0, return; end
thresh = mas*10^(cutoff/20); % db to linear
toosmall = find(as < thresh);
clipped = s;
clipped(toosmall) = thresh;

Matlab listing: mps.m and test program

This section lists and describes the Matlab/Octave function mps which estimates a minimum-phase spectrum given only the spectral magnitude. A test program for mps together with a listing of its output are given in §J.11 below. See §11.7 for related discussion.

Matlab listing: mps.m

function [sm] = mps(s)
% [sm] = mps(s)
% create minimum-phase spectrum sm from complex spectrum s
   sm = exp( fft( fold( ifft( log( clipdb(s,-100) )))));

Note that mps.m must be given a whole spectrum in ``FFT buffer format''. That is, it must contain dc and positive-frequency values followed by negative frequency values and be a power of 2 in length.

The mps function works well as long as the desired frequency response is smooth. If there are any zeros on the frequency axis (``notches''), the corresponding minimum-phase impulse response will be time aliased because the corresponding exponentials in the cepstrum never decay. To suppress time-aliasing to some extent, the desired frequency response magnitude is clipped to 100 dB below its maximum. Time aliasing can be reduced by interpolating the desired frequency response s to a higher sampling density (thereby increasing the time available for exponential decay in the cepstral domain). However, for pure notches (zeros right on the unit circle), no amount of oversampling will eliminate the time aliasing completely. To avoid time aliasing in the cepstrum, such a desired spectrum must be smoothed before taking the log and inverse FFT. Zero-phase smoothing of the spectral magnitude is a typical choice for this purpose. When greater accuracy is required, all notch frequencies can be estimated so that terms of the form can be effectively ``divided out'' of the desired spectrum and carried along as separate factors.

Matlab listing: tmps.m

Below is the test script (for ease of copy/paste extraction for online viewers). Following is the test script along with its output.

Note that this is a toy example intended only for checking the code on a simple example, and to illustrate how a spectrum gets passed in. In particular, the would-be minimum-phase impulse response computed by this example is clearly not even causal (thus indicating an insufficient spectral sampling density [FFT length]). Moreover, the starting spectrum (a sampled ideal lowpass-filter frequency response) has zeros on the unit circle, so there is no sampling density that is truly sufficient in the frequency domain (no sufficiently long FFT in the time domain).

spec = [1 1 1 0 0 0 1 1]'; % Lowpass cutting off at fs*3/8
format short;
mps(spec)
abs(mps(spec))
ifft(spec)
ifft(mps(spec))

Matlab diary: tmps.d

Below is the output of the test script with echo on in Matlab.

spec = [1 1 1 0 0 0 1 1]'; % Lowpass cutting off at fs*3/8
format short;
mps(spec)

ans =
   1.0000 - 0.0000i
   0.3696 - 0.9292i
  -0.2830 - 0.9591i
   0.0000 - 0.0000i
   0.0000 + 0.0000i
   0.0000 + 0.0000i
  -0.2830 + 0.9591i
   0.3696 + 0.9292i

abs(mps(spec))

ans =
    1.0000
    1.0000
    1.0000
    0.0000
    0.0000
    0.0000
    1.0000
    1.0000

ifft(spec)

ans =
   0.6250
   0.3018 - 0.0000i
  -0.1250
  -0.0518 - 0.0000i
   0.1250
  -0.0518 + 0.0000i
  -0.1250
   0.3018 + 0.0000i

ifft(mps(spec))

ans =
   0.1467 - 0.0000i
   0.5944 - 0.0000i
   0.4280 - 0.0000i
  -0.0159 - 0.0000i
  -0.0381 - 0.0000i
   0.1352 - 0.0000i
  -0.0366 - 0.0000i
  -0.2137 - 0.0000i

Signal Plots: swanalplot.m

Figure J.13 lists a Matlab script for plotting input and output signals for the simplest lowpass filter in §2.2, used in Fig.2.4 to produce Fig.2.5. This is not really a ``utility'' since it relies on global variables. It is instead a script containing mundane plotting code that was omitted from Fig.2.4 to make it fit on one page. I include it only because people keep asking for it! The script is compatible with Matlab only.

%swanalplot.m - plots needed by swanal.m

doplots = 1; % set to 0 to skip plots
dopause = 0; % set to 1 to pause after each plot
if doplots
  figure(gcf);
  subplot(2,1,1);
  ttl=sprintf('Filter Input Sinusoid, f(%d)=%0.2f',k,f(k));
  myplot(t,s,'*k',ttl);
  tinterp=0:(t(2)-t(1))/10:t(end); % interpolated time axis
  si = ampin*cos(2*pi*f(k)*tinterp+phasein); % for plot
  text(-1.5,0,'(a)');
  hold on; plot(tinterp,si,'--k'); hold off;
  subplot(2,1,2);
  ttl='Filter Output Sinusoid';
  myplot(t,y,'*k',ttl);
  text(-1.5,0,'(b)');
  if dopause, disp('PAUSING - [RETURN] to continue . . .');
  pause; end
  saveplot(sprintf('../eps/swanal-%d.eps',k));
end

Frequency Response Plot: swanalmainplot.m

Figure J.14 lists a Matlab script for plotting (in Fig.2.7) the overlay of the theoretical frequency response with that measured using simulated sine-wave analysis for the case of the simplest lowpass filter. It is written to run in the specific context of the matlab script listed in Fig.2.3 of §2.2. This is not a general-purpose ``utility'' because it relies on global variables defined in the calling script. This script is included only for completeness and is compatible with Matlab only.

% swanalmainplot.m
% Compare measured and theoretical frequency response.
% This script is invoked by swanalmainplot.m and family,
% and requires context set up by the caller.

figure(N+1); % figure number is arbitary

subplot(2,1,1);
ttl = 'Amplitude Response';
freqplot(f,gains,'*k',ttl,'Frequency (Hz)','Gain');
tar = 2*cos(pi*f/fs); % theoretical amplitude response
hold on; freqplot(f,tar,'-k'); hold off;
text(-0.08,mean(ylim),'(a)');

subplot(2,1,2);
ttl = 'Phase Response';
tpr = -pi*f/fs; % theoretical phase response
pscl = 1/(2*pi);% convert radian phase shift to cycles
freqplot(f,tpr*pscl,'-k',ttl,'Frequency (cycles)',...
	'Phase shift (cycles)');
hold on; freqplot(f,phases*pscl,'*k'); hold off;
text(-0.08,mean(ylim),'(b)');
saveplot(plotfile); % set by caller

Sign in