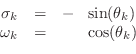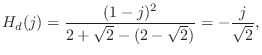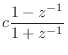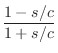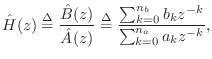Recursive Digital Filter Design
The subject of digital filter design is enormous--much larger than we can hope to address in this book. However, a surprisingly large number of applications can be addressed using small filter sections which are easily designed by hand, as exemplified in Appendix B. This appendix describes some of the ``classic'' methods for IIR filter design based on the bilinear transformation of prototype analog filters, followed by the simple but powerful weighted equation error method for general purpose IIR design. For further information on digital filter design, see the documentation for the Matlab Toolboxes for Signal Processing and Filter Design, and/or [64,68,60,78].
Lowpass Filter Design
We have discussed in detail (Chapter 1) the simplest lowpass filter,
![]() having the transfer function
having the transfer function
![]() with
one zero at
with
one zero at ![]() and one pole at
and one pole at ![]() . From the graphical method
for visualizing the amplitude response (§8.2), we see that this
filter totally rejects signal energy at half the sampling rate, while
lower frequencies experience higher gains, reaching a maximum at
. From the graphical method
for visualizing the amplitude response (§8.2), we see that this
filter totally rejects signal energy at half the sampling rate, while
lower frequencies experience higher gains, reaching a maximum at
![]() . We also see that the pole at
. We also see that the pole at ![]() has no effect on the
amplitude response.
has no effect on the
amplitude response.
A high quality lowpass filter should look more like the ``box car'' amplitude response shown in Fig.1.1. While it is impossible to achieve this ideal response exactly using a finite-order filter, we can come arbitrarily close. We can expect the amplitude response to improve if we add another pole or zero to the implementation.
Perhaps the best known ``classical'' methods for lowpass filter designs are those derived from analog Butterworth, Chebyshev, and Elliptic Function filters [64]. These generally yield IIR filters with the same number of poles as zeros. When an FIR lowpass filter is desired, different design methods are used, such as the window method [68, p. 88] (Matlab functions fir1 and fir2), Remez exchange algorithm [68, pp. 136-140], [64, pp. 89-106] (Matlab functions remez and cremez), linear programming [93], [68, p. 140], and convex optimization [67]. This section will describe only Butterworth IIR lowpass design in some detail. For the remaining classical cases (Chebyshev, Inverse Chebyshev, and Elliptic), see, e.g., [64, Chapter 7] and/or Matlab/Octave functions butter, cheby1, cheby2, and ellip.
Butterworth Lowpass Design
Almost all methods for filter design are optimal in some sense,
and the choice of optimality determines nature of the design.
Butterworth filters are optimal in the sense of having a
maximally flat amplitude response, as measured using a Taylor
series expansion about dc [64, p. 162]. Of course,
the trivial filter ![]() has a perfectly flat amplitude response,
but that's an allpass, not a lowpass filter. Therefore, to constrain the
optimization to the space of lowpass filters, we need
constraints on the design, such as
has a perfectly flat amplitude response,
but that's an allpass, not a lowpass filter. Therefore, to constrain the
optimization to the space of lowpass filters, we need
constraints on the design, such as ![]() and
and ![]() .
That is, we may require the dc gain to be 1, and the gain at half the
sampling rate to be 0.
.
That is, we may require the dc gain to be 1, and the gain at half the
sampling rate to be 0.
It turns out Butterworth filters (as well as Chebyshev and Elliptic
Function filter types) are much easier to design as analog
filters which are then converted to digital filters. This means
carrying out the design over the ![]() plane instead of the
plane instead of the ![]() plane,
where the
plane,
where the ![]() plane is the complex plane over which analog filter
transfer functions are defined. The analog transfer function
plane is the complex plane over which analog filter
transfer functions are defined. The analog transfer function ![]() is very much like the digital transfer function
is very much like the digital transfer function ![]() , except that it
is interpreted relative to the analog frequency axis
, except that it
is interpreted relative to the analog frequency axis
![]() (the ``
(the ``![]() axis'') instead of the digital frequency axis
axis'') instead of the digital frequency axis
![]() (the ``unit circle''). In particular, analog filter poles
are stable if and only if they are all in the left-half of the
(the ``unit circle''). In particular, analog filter poles
are stable if and only if they are all in the left-half of the
![]() plane, i.e., their real parts are negative. An
introduction to Laplace transforms is given in Appendix D, and an
introduction to converting analog transfer functions to digital
transfer functions using the bilinear transform appears in
§I.3.
plane, i.e., their real parts are negative. An
introduction to Laplace transforms is given in Appendix D, and an
introduction to converting analog transfer functions to digital
transfer functions using the bilinear transform appears in
§I.3.
Butterworth Lowpass Poles and Zeros
When the maximally flat optimality criterion is applied to the general
(analog) squared amplitude response
![]() , a surprisingly simple
result is obtained [64]:
, a surprisingly simple
result is obtained [64]:
where
The analytic continuation
(§D.2)
of
![]() to the whole
to the whole
![]() -plane may be obtained by substituting
-plane may be obtained by substituting
![]() to obtain
to obtain

with
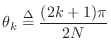
A Butterworth lowpass filter additionally has ![]() zeros at
zeros at ![]() .
Under the bilinear transform
.
Under the bilinear transform
![]() , these all map to the
point
, these all map to the
point ![]() , which determines the numerator of the digital filter as
, which determines the numerator of the digital filter as
![]() .
.
Given the poles and zeros of the analog prototype, it is straightforward to convert to digital form by means of the bilinear transformation.
Example: Second-Order Butterworth Lowpass
In the second-order case, we have, for the analog prototype,
To convert this to digital form, we apply the bilinear transform
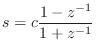
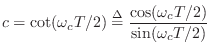
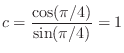
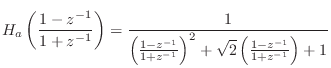 |
(I.4) | ||
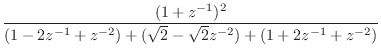 |
(I.5) | ||
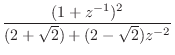 |
(I.6) | ||
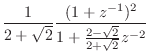 |
(I.7) |
Note that the numerator is

In the analog prototype,
the cut-off frequency is
![]() rad/sec, where,
from Eq.
rad/sec, where,
from Eq.![]() (I.1), the amplitude response
is
(I.1), the amplitude response
is
![]() . Since we mapped the cut-off frequency precisely
under the bilinear transform, we expect the digital filter to have
precisely this gain.
The digital frequency response at one-fourth the sampling rate is
. Since we mapped the cut-off frequency precisely
under the bilinear transform, we expect the digital filter to have
precisely this gain.
The digital frequency response at one-fourth the sampling rate is
and
Note from Eq.![]() (I.8) that the phase at cut-off is exactly -90 degrees
in the digital filter. This can be verified against the pole-zero
diagram in the
(I.8) that the phase at cut-off is exactly -90 degrees
in the digital filter. This can be verified against the pole-zero
diagram in the ![]() plane, which has two zeros at
plane, which has two zeros at ![]() , each
contributing +45 degrees, and two poles at
, each
contributing +45 degrees, and two poles at
![]() , each contributing -90
degrees. Thus, the calculated phase-response at the cut-off frequency
agrees with what we expect from the digital pole-zero diagram.
, each contributing -90
degrees. Thus, the calculated phase-response at the cut-off frequency
agrees with what we expect from the digital pole-zero diagram.
In the ![]() plane, it is not as easy to use the pole-zero diagram
to calculate the phase at
plane, it is not as easy to use the pole-zero diagram
to calculate the phase at
![]() , but using Eq.
, but using Eq.![]() (I.3), we
quickly obtain
(I.3), we
quickly obtain
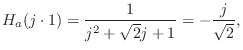
A related example appears in §9.2.4.
Digitizing Analog Filters with the
Bilinear Transformation
The desirable properties of many filter types (such as lowpass,
highpass, and bandpass) are preserved very well by the
![]() mapping called the bilinear transform.
mapping called the bilinear transform.
Bilinear Transformation
The bilinear transform may be defined by
where
Frequency Warping
It is easy to check that the bilinear transform gives a one-to-one,
order-preserving, conformal map [57] between the
analog frequency axis
![]() and the digital frequency axis
and the digital frequency axis
![]() , where
, where ![]() is the sampling interval. Therefore, the
amplitude response takes on exactly the same values over both axes,
with the only defect being a
frequency warping such
that equal increments along the unit circle in the
is the sampling interval. Therefore, the
amplitude response takes on exactly the same values over both axes,
with the only defect being a
frequency warping such
that equal increments along the unit circle in the ![]() plane
correspond to larger and larger bandwidths along the
plane
correspond to larger and larger bandwidths along the ![]() axis in
the
axis in
the ![]() plane [88]. Some kind of frequency warping
is obviously unavoidable in any one-to-one map because the analog
frequency axis is infinite while the digital frequency axis is finite.
The relation between the analog and digital frequency axes may be
derived immediately from Eq.
plane [88]. Some kind of frequency warping
is obviously unavoidable in any one-to-one map because the analog
frequency axis is infinite while the digital frequency axis is finite.
The relation between the analog and digital frequency axes may be
derived immediately from Eq.![]() (I.9) as
(I.9) as
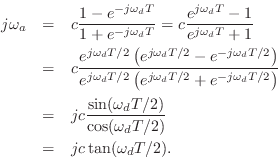
Given an analog cut-off frequency
![]() , to obtain the
same cut-off frequency in the digital filter, we set
, to obtain the
same cut-off frequency in the digital filter, we set
Analog Prototype Filter
Since the digital cut-off frequency may be set to any value,
irrespective of the analog cut-off frequency, it is convenient to set
the analog cut-off frequency to
![]() . In this case, the
bilinear-transform constant
. In this case, the
bilinear-transform constant ![]() is simply set to
is simply set to
Examples
Examples of using the bilinear transform to ``digitize'' analog filters may be found in §I.2 and [64,5,6,103,86]. Bilinear transform design is also inherent in the construction of wave digital filters [25,86].
Filter Design by Minimizing the
L2 Equation-Error Norm
One of the simplest formulations of recursive digital filter design is based on minimizing the equation error. This method allows matching of both spectral phase and magnitude. Equation-error methods can be classified as variations of Prony's method [48]. Equation error minimization is used very often in the field of system identification [46,30,78].
The problem of fitting a digital filter to a given spectrum may be formulated as follows:
Given a continuous complex function
![]() ,
corresponding to a causalI.2 desired
frequency-response, find a stable digital filter of the form
,
corresponding to a causalI.2 desired
frequency-response, find a stable digital filter of the form
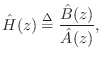
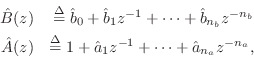
with
![]() given, such that some norm of the error
given, such that some norm of the error
![$\displaystyle \hat{\theta}^T\isdef \left[\hat{b}_0,\hat{b}_1,\ldots\,,\hat{b}_{{n}_b},\hat{a}_1,\hat{a}_2,\ldots\,,\hat{a}_{{n}_a}\right]^T,
$](http://www.dsprelated.com/josimages_new/filters/img2389.png)
The approximate filter ![]() is typically constrained to be stable,
and since positive powers of
is typically constrained to be stable,
and since positive powers of ![]() do not appear in
do not appear in
![]() , stability
implies causality. Consequently, the impulse response of the filter
, stability
implies causality. Consequently, the impulse response of the filter
![]() is zero for
is zero for ![]() . If
. If ![]() were noncausal, all impulse-response components
were noncausal, all impulse-response components
![]() for
for ![]() would be approximated by zero.
would be approximated by zero.
Equation Error Formulation
The equation error is defined (in the frequency domain) as
By comparison, the more natural frequency-domain error is the so-called output error:
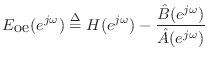
The names of these errors make the most sense in the time domain. Let
![]() and
and ![]() denote the filter input and output, respectively, at time
denote the filter input and output, respectively, at time
![]() . Then the equation error is the error in the difference equation:
. Then the equation error is the error in the difference equation:
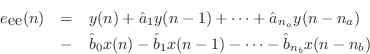
while the output error is the difference between the ideal and approximate filter outputs:
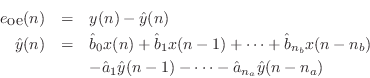
Denote the ![]() norm of the equation error by
norm of the equation error by
where
Note that (I.11) can be expressed as
Error Weighting and Frequency Warping
Audio filter designs typically benefit from an error weighting
function that weights frequencies according
to their audibility. An oversimplified but useful weighting function
is simply ![]() , in which low frequencies are deemed generally
more important than high frequencies. Audio filter designs also
typically improve when using a frequency warping, such as
described in [88,78] (and similar to that
in §I.3.2). In principle, the effect of a frequency-warping can
be achieved using a weighting function, but in practice, the numerical
performance of a frequency warping is often much better.
, in which low frequencies are deemed generally
more important than high frequencies. Audio filter designs also
typically improve when using a frequency warping, such as
described in [88,78] (and similar to that
in §I.3.2). In principle, the effect of a frequency-warping can
be achieved using a weighting function, but in practice, the numerical
performance of a frequency warping is often much better.
Stability of Equation Error Designs
A problem with equation-error methods is that stability of the filter
design is not guaranteed. When an unstable design is encountered,
one common remedy is to reflect unstable poles inside the unit circle,
leaving the magnitude response unchanged while modifying the phase of the
approximation in an ad hoc manner. This requires polynomial factorization
of
![]() to find the filter poles, which is typically more work
than the filter design itself.
to find the filter poles, which is typically more work
than the filter design itself.
A better way to address the instability problem is to repeat the
filter design employing a bulk delay. This amounts to
replacing
![]() by
by
Unstable equation-error designs are especially likely when
![]() is
noncausal. Since there are no constraints on where the poles of
is
noncausal. Since there are no constraints on where the poles of
![]() can be, one can expect unstable designs for desired
frequency-response functions having a linear phase trend with positive
slope.
can be, one can expect unstable designs for desired
frequency-response functions having a linear phase trend with positive
slope.
In the other direction, experience has shown that best results are obtained
when ![]() is minimum phase, i.e., when all the zeros of
is minimum phase, i.e., when all the zeros of ![]() are
inside the unit circle. For a given magnitude,
are
inside the unit circle. For a given magnitude,
![]() ,
minimum phase gives the maximum concentration of impulse-response energy
near the time origin
,
minimum phase gives the maximum concentration of impulse-response energy
near the time origin ![]() . Consequently, the impulse-response tends to start
large and decay immediately. For non-minimum phase
. Consequently, the impulse-response tends to start
large and decay immediately. For non-minimum phase ![]() , the
impulse-response
, the
impulse-response ![]() may be small for the first
may be small for the first ![]() samples, and the
equation error method can yield very poor filters in these cases. To see
why this is so, consider a desired impulse-response
samples, and the
equation error method can yield very poor filters in these cases. To see
why this is so, consider a desired impulse-response ![]() which is zero
for
which is zero
for
![]() , and arbitrary thereafter. Transforming
, and arbitrary thereafter. Transforming ![]() into the
time domain yields
into the
time domain yields
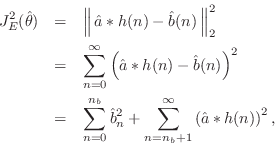
where ``![]() '' denotes convolution, and the additive decomposition
is due the fact that
'' denotes convolution, and the additive decomposition
is due the fact that
![]() for
for
![]() . In this case the
minimum occurs for
. In this case the
minimum occurs for
![]() ! Clearly this is
not a particularly good fit. Thus, the introduction of bulk-delay to guard
against unstable designs is limited by this phenomenon.
! Clearly this is
not a particularly good fit. Thus, the introduction of bulk-delay to guard
against unstable designs is limited by this phenomenon.
It should be emphasized that for minimum-phase
![]() ,
equation-error methods are very effective. It is simple to convert a
desired magnitude response into a minimum-phase frequency-response
by use of cepstral techniques [22,60] (see also the
appendix below), and this is highly recommended when minimizing equation
error. Finally, the error weighting by
,
equation-error methods are very effective. It is simple to convert a
desired magnitude response into a minimum-phase frequency-response
by use of cepstral techniques [22,60] (see also the
appendix below), and this is highly recommended when minimizing equation
error. Finally, the error weighting by
![]() can usually be
removed by a few iterations of the Steiglitz-McBride algorithm.
can usually be
removed by a few iterations of the Steiglitz-McBride algorithm.
An FFT-Based Equation-Error Method
The algorithm below minimizes the equation error in the frequency-domain. As a result, it can make use of the FFT for speed. This algorithm is implemented in Matlab's invfreqz() function when no iteration-count is specified. (The iteration count gives that many iterations of the Steiglitz-McBride algorithm, thus transforming equation error to output error after a few iterations. There is also a time-domain implementation of the Steiglitz-McBride algorithm called stmcb() in the Matlab Signal Processing Toolbox, which takes the desired impulse response as input.)
Given a desired spectrum
![]() at equally spaced frequencies
at equally spaced frequencies
![]() , with
, with ![]() a power of
a power of ![]() ,
it is desired to find a rational digital
filter with
,
it is desired to find a rational digital
filter with ![]() zeros and
zeros and ![]() poles,
poles,
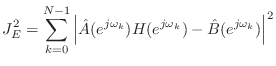
Since ![]() is a quadratic form, the solution is readily obtained by
equating the gradient to zero. An easier derivation follows from minimizing
equation error variance in the time domain and making use of the orthogonality
principle [36].
This may be viewed as a system identification problem where the
known input signal is an impulse, and the known output is the desired
impulse response. A formulation employing an arbitrary known input
is valuable for introducing complex weighting across the frequency grid,
and this general form is presented. A detailed derivation appears in
[78, Chapter 2], and here only the final algorithm is given:
is a quadratic form, the solution is readily obtained by
equating the gradient to zero. An easier derivation follows from minimizing
equation error variance in the time domain and making use of the orthogonality
principle [36].
This may be viewed as a system identification problem where the
known input signal is an impulse, and the known output is the desired
impulse response. A formulation employing an arbitrary known input
is valuable for introducing complex weighting across the frequency grid,
and this general form is presented. A detailed derivation appears in
[78, Chapter 2], and here only the final algorithm is given:
Given spectral output samples
![]() and input
samples
and input
samples
![]() , we minimize
, we minimize
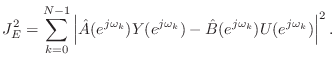
Let
![]() :
:![]() denote the column vector determined
by
denote the column vector determined
by ![]() , for
, for
![]() filled in from top to bottom, and let
filled in from top to bottom, and let
![]() :
:![]() denote the size
denote the size ![]() symmetric Toeplitz matrix consisting of
symmetric Toeplitz matrix consisting of
![]() :
:![]() in its first column.
A nonsymmetric Toeplitz matrix may be specified by its first column and row,
and we use the notation
in its first column.
A nonsymmetric Toeplitz matrix may be specified by its first column and row,
and we use the notation
![]() :
:![]() :
:![]() to denote the
to denote the
![]() by
by ![]() Toeplitz matrix with left-most column
Toeplitz matrix with left-most column
![]() :
:![]() and top row
and top row
![]() :
:![]() .
The inverse Fourier transform of
.
The inverse Fourier transform of
![]() is defined as
is defined as
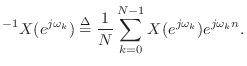
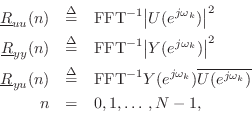
where the overbar denotes complex conjugation, and four corresponding Toeplitz matrices,
![\begin{eqnarray*}
R_{yy} &\isdef & T(\underline{R}_{yy}[0\,\mbox{:}\,{{n}_a}-1])...
...u}^T[-1\,\mbox{:}\,-{{n}_a}])\\
R_{uy} &\isdef & R_{uy}^T , \\
\end{eqnarray*}](http://www.dsprelated.com/josimages_new/filters/img2450.png)
where negative indices are to be interpreted mod ![]() , e.g.,
, e.g.,
![]() .
.
The solution is then
![$\displaystyle \hat{\theta}^\ast = \left[\begin{array}{c} \underline{\hat{B}}^\a...
...,{{n}_b}] \\ [2pt] \underline{R}_{yy}[1\,\mbox{:}\,{{n}_a}] \end{array}\right]
$](http://www.dsprelated.com/josimages_new/filters/img2452.png)
![$\displaystyle \underline{\hat{B}}^\ast \isdef \left[\begin{array}{c} \hat{b}^\a...
...t{a}^\ast _0 \\ [2pt] \vdots \\ [2pt] \hat{a}^\ast _{{n}_a}\end{array}\right],
$](http://www.dsprelated.com/josimages_new/filters/img2453.png)
Prony's Method
There are several variations on equation-error minimization, and some
confusion in terminology exists. We use the definition of Prony's
method given by Markel and Gray [48]. It is equivalent to ``Shank's
method'' [9]. In this method, one first computes the
denominator
![]() by minimizing
by minimizing
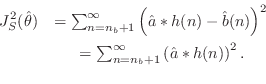
This step is equivalent to minimization of ratio error
(as used in linear prediction) for the
all-pole part
![]() , with the first
, with the first ![]() terms of the time-domain
error sum discarded (to get past the influence of the zeros
on the impulse response). When
terms of the time-domain
error sum discarded (to get past the influence of the zeros
on the impulse response). When
![]() , it coincides with the
covariance method of linear prediction [48,47]. This idea for
finding the poles by ``skipping'' the influence of the zeros on the
impulse-response shows up in the stochastic case under the name of modified Yule-Walker equations [11].
, it coincides with the
covariance method of linear prediction [48,47]. This idea for
finding the poles by ``skipping'' the influence of the zeros on the
impulse-response shows up in the stochastic case under the name of modified Yule-Walker equations [11].
Now, Prony's method consists of next minimizing ![]() output error
with the pre-assigned poles given by
output error
with the pre-assigned poles given by
![]() . In other words, the
numerator
. In other words, the
numerator
![]() is found by minimizing
is found by minimizing
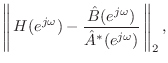
The Padé-Prony Method
Another variation of Prony's method, described by Burrus and Parks
[9] consists of using Padé approximation to
find the numerator
![]() after the denominator
after the denominator
![]() has been found
as before. Thus,
has been found
as before. Thus,
![]() is found by matching the first
is found by matching the first ![]() samples of
samples of ![]() , viz.,
, viz.,
![]() . This method is faster, but does not generally give
as good results as the previous version. In particular, the degenerate
example
. This method is faster, but does not generally give
as good results as the previous version. In particular, the degenerate
example
![]() gives
gives
![]() here as did pure
equation error. This method has been applied also in the stochastic
case [11].
here as did pure
equation error. This method has been applied also in the stochastic
case [11].
On the whole, when
![]() is causal and minimum phase (the ideal
situation for just about any stable filter-design method), the
variants on equation-error minimization described in this section
perform very similarly. They are all quite fast, relative to
algorithms which iteratively minimize output error, and the
equation-error method based on the FFT above is generally fastest.
is causal and minimum phase (the ideal
situation for just about any stable filter-design method), the
variants on equation-error minimization described in this section
perform very similarly. They are all quite fast, relative to
algorithms which iteratively minimize output error, and the
equation-error method based on the FFT above is generally fastest.
Next Section:
Matlab Utilities
Previous Section:
A View of Linear Time Varying Digital Filters