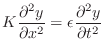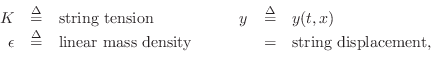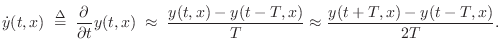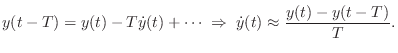A History of Enabling Ideas Leading to Virtual Musical Instruments
This appendix summarizes some milestones toward the development of virtual musical instruments. Beginning with early musical acoustics, key developments in the literature deemed most enabling for virtual acoustic instruments are traced up to the mid 1980s, with an emphasis on string models (as in the text overall). Selected follow-on efforts are mentioned. A condensed version of this appendix was published in [446], with associated presentation overheads [448].
Early Musical Acoustics
All things which can be known have number; for it is not possible that without number anything can be either conceived or known.
-- Philolaus (ca. 400 BC)
Vibrating strings were studied by the Pythagoreans (6th-5th century BC). Pythagorus noticed that harmonics were produced by dividing the string length by whole numbers, and he was interested in understanding consonant pitch intervals in terms of simple ratios of string lengths. ``Harmony theory'' from the Pythagoreans was taught throughout the Middle Ages as one of the seven liberal arts: the quadrivium, consisting of arithmetic, geometry, astronomy, and music (harmony theory); and the trivium, consisting of grammar, logic, and rhetoric [411]. The correspondence between musical pitch and frequency of physical vibration was not discovered until the seventeenth century [113].
It took until Galileo (1564-1642) to be free of the formulation of
Aristotle (384-322 BC) that all motion required an ongoing applied
force, thereby opening the way for modern differential equations of
motion. The ideas of Galileo were formalized and extended by Newton
(1642-1727), whose famous second law of motion ``![]() '' lies at the
foundation of essentially all classical mechanics and acoustics.
Newton's Principia (1686) describes sound as traveling
pressure pulses, and single-frequency sound waves were analyzed.
'' lies at the
foundation of essentially all classical mechanics and acoustics.
Newton's Principia (1686) describes sound as traveling
pressure pulses, and single-frequency sound waves were analyzed.
The first to publish a one-dimensional wave equation for the vibrating string was the applied mathematician Jean Le Rond d'Alembert (1717-1783) [100,103].A.1The 1D wave equation can be written as
where
where
History of Modal Expansion
While the traveling-wave solution for the ideal vibrating string is fully general, and remains the basis for the most efficient known string synthesis algorithms, an important alternate formulation is in terms of modal expansions, that is, a superposition sum of orthogonal basis functions which solve the differential equation and obey the boundary conditions. Daniel Bernoulli (1700-1782) developed the notion that string vibrations can be expressed as the superposition of an infinite number of harmonic vibrations [103].A.5This approach ultimately evolved to Hilbert spaces of orthogonal basis functions that are solutions of Hermitian linear operators--a formulation at the heart of quantum mechanics describing what can be observed in nature [112,539]. In computational acoustic modeling, Sturm-Liouville theory has been used to give improved models of nonuniform acoustic tubes such as horns [50], and to provide spatial transforms analogous to the Laplace transform [360].
In the field of computer music, the introduction of modal synthesis is credited to Adrien [5]. More generally, a modal synthesis model is perhaps best formulated via a diagonalized state-space formulation [558,220,107].A.6 A more recent technique, which has also been used to derive modal synthesis models, is the so-called functional transformation method [360,499,498]. In this approach, physically meaningful transfer functions are mapped from continuous to discrete time in a way which preserves desired physical parametric controls.
Mass-Spring Resonators
Since a harmonic oscillator is produced by a simple mass-spring
system, a mechanical generator for the harmonic basis functions of
Bernoulli
is readily obtained by equating Newton's second law
![]() for
the reaction force of an ideal mass
for
the reaction force of an ideal mass ![]() , with Robert Hooke's spring
force law
, with Robert Hooke's spring
force law ![]() (published in 1676), where
(published in 1676), where ![]() is an empirical
spring constant [65]. Hooke (1635-1703) was a contemporary
of Newton's who carried out extensive experiments with springs in
search of a spring-regulated clock [259, pp. 274-288].
Hooke's law was generalized to 3D by Cauchy (1789-1857) as the
familiar linear relationship between six components of stress
and
strain.A.7
is an empirical
spring constant [65]. Hooke (1635-1703) was a contemporary
of Newton's who carried out extensive experiments with springs in
search of a spring-regulated clock [259, pp. 274-288].
Hooke's law was generalized to 3D by Cauchy (1789-1857) as the
familiar linear relationship between six components of stress
and
strain.A.7
Elementary mass-spring models have found much use in computational physical models for purposes of sound synthesis [69,92]. For example, a mass-spring oscillator is typically used to model a brass-player's lips [4], piano hammers [44], and is sometimes included in woodwind-reed models [406].
Sampling Theory
Nowadays, audio processing is typically carried out in discrete time. As a result, sampling theory is fundamental to digital audio signal processing. The sampling theorem is credited to Harold Nyquist (1928), extending an earlier result by Cauchy (1831) based on series expansions. Claude Shannon is credited with reviving interest in the sampling theorem after World War II when computers became public.A.8 As a result, the sampling theorem is often called ``Nyquist's sampling theorem,'' ``Shannon's sampling theorem,'' or the like. The sampling rate has been called the ``Nyquist rate'' in honor of Nyquist's contributions [333]. Often in common usage, however, the term ``Nyquist rate'' is used to refer instead to half the sampling rate. To preserve the historically correct meaning, we might encourage use of the term Nyquist limit to mean half the sampling rate, and simply say ``sampling rate'' instead of ``Nyquist rate'', so as to minimize confusion.
Physical Digital Filters
Analog Computers
Analog filters are inherently ``physical'' since voltages and currents are direct ``analogs'' for physical variables such as force and velocity. So-called ``analog computers'' were often used for physical system simulation before digital computers took over.
Finite Difference Methods
One of the first applications of digital computers to numerical
simulation of physical systems was the so-called finite
difference approach [481].
The general
procedure is to replace derivatives by finite differences, and there
are many variations on how this can be done. For example, the first
partial derivative with respect to time in Eq.![]() (A.1) may be
approximated by
(A.1) may be
approximated by
The second form, called a centered finite difference, has the advantage of not introducing a time delay, but at the expense of requiring an extra factor of two oversampling for a given accuracy in its magnitude response (when viewed as a digital filter).
Finite differences are at least as old as Taylor series, since,
Interestingly, the general Taylor series, published in 1715 by Taylor in his book Methodus Incrementorum Directa et Inversa, was known more than forty years earlier to James Gregory (1668), somewhat earlier to Jean Bernoulli, and to some extent even before 1550 in India [65, pp. 422,469].
Finite differences were used to construct the earliest known digital models of vibrating strings by Pierre Ruiz and Lejaren Hiller ca. 1971 [194].
Finite-difference methods have not historically been aimed at real-time simulation, and they are generally used with very large sampling rates compared with the ``band of interest''. On the order of ten-times oversampling is needed to obtain reasonably accurate simulation across the entire audio band when using classical finite difference methods. In the finite-difference method literature, accuracy is usually only considered at dc, which is inaudible. Since finite difference models are usually linear, time-invariant digital filters, it is straightforward to improve them by filter-design methods, optimizing perceived audio error over the entire audio band. Such improved (and optionally extended) coefficients can then be used to construct a refined, indirectly estimated, partial differential equation.
Other offline (slower than real time) computational physical modeling methods include finite element [480] and boundary element methods. Such offline simulations can be valuable as a source of ``virtual experiments'' which enable the testing and calibration of faster algorithms. As an example, a detailed simulation of guitar acoustics, employing both finite difference and finite element modeling approaches, is reported in [109].
Transfer Function Models
As indicated in the previous section, instead of digitizing a differential equation by finite differences, one can often formulate a filter design problem. This is ideal when all that matters is the input-output response of the physical system, and the physical system is linear and time-invariant (LTI). When the desired transfer function spans more than one system element, non-physical models are usually obtained, so we will not consider such models further. However, digital filter design methods optimizing perceptually motivated error criteria are extremely effective in spectral modeling and audio compression applications [337]. They are also good choices for subsystems which are to remain fixed over time, such as cello bodies, piano soundboards, and the like.
Wave Digital Filter Models
Perhaps the best known physics-based approach to digital filter design is wave digital filters, developed principally by Alfred Fettweis [136].A.9Wave digital filters may be constructed by applying the bilinear transform [343] to the scattering-theoretic formulation of lumped RLC networks introduced in circuit theory by Vitold Belevitch [34]. Fettweis in fact worked with Belevitch.A.10Scattering theory had been in use for many years prior in quantum mechanics.
A key, driving property of wave digital filters is low sensitivity to coefficient round-off error. This follows from the correspondence to passive circuit networks. Wave digital filters also have the nice property of preserving order of the original (analog) system. For example, a ``wave digital spring'' is simply a unit delay, and a ``wave digital mass'' is a unit delay with a sign flip. The only approximation aspect is the frequency-warping caused by the bilinear transform. It is interesting to note that when it is possible to frequency-warp input/output signals exactly, a wave digital filter can implement a continuous-time LTI system exactly! See [55] for a discussion of wave digital filters and their relation to finite differences et al.
In computer music, various ``wave digital elements'' have been proposed, including wave digital toneholes [527], piano hammers [56], and woodwind bores [525].
Voice Synthesis
Unquestionably, the most extensive prior work in the 20th century relevant to virtual acoustic musical instruments occurred within the field of speech synthesis [139,142,363,408,335,106,243].A.11 This research was driven by both academic interest and the potential practical benefits of speech compression to conserve telephone bandwidth. It was clear at an early point that the bandwidth of a telephone channel (nominally 200-3200 Hz) was far greater than the ``information rate'' of speech. It was reasoned, therefore, that instead of encoding the speech waveform, it should be possible to encode instead more slowly varying parameters of a good synthesis model for speech.
Before the 20th century, there were several efforts to simulate the voice mechanically, going back at least until 1779 [140].
Dudley's Vocoder
The first major effort to encode speech electronically was Homer Dudley's vocoder (``voice coder'') [119] developed starting in October of 1928 at AT&T Bell Laboratories [414]. A manually controlled version of the vocoder synthesis engine, called the Voder (Voice Operation Demonstrator [140]), was constructed and demonstrated at the 1939 World's Fairs in New York and San Francisco [119]. Pitch was controlled by a foot pedal, and ten fingers controlled the bandpass gains. Buzz/hiss selection was by means of a wrist bar. Three additional keys controlled transient excitation of selected filters to achieve stop-consonant sounds [140]. ``Performing speech'' on the Voder required on the order of a year's training before intelligible speech could reliably be produced. The Voder was a very interesting performable instrument!
The vocoder and Voder can be considered based on a
source-filter model for speech which includes a
non-parametric spectral model of the vocal tract given by the
output of a fixed bandpass-filter-bank over time. Later efforts
included the formant vocoder (Munson and Montgomery 1950)--a
type of parametric spectral model--which encoded ![]() and the
amplitude and center-frequency of the first three spectral
formants. See [306, p. 2452-3] for an overview
and references.
and the
amplitude and center-frequency of the first three spectral
formants. See [306, p. 2452-3] for an overview
and references.
While we have now digressed to into the realm of spectral models, as opposed to physical models, it seems worthwhile to point out that the early efforts toward speech synthesis were involved with essentially all of the mainstream sound modeling methods in use today (both spectral and physical domains).
Vocal Tract Analog Models
There is one speech-synthesis thread that clearly classifies under
computational physical modeling, and that is the topic of vocal
tract analog models. In these models, the vocal tract is regarded as
a piecewise cylindrical acoustic tube. The first mechanical
analogue of an acoustic-tube model appears to be a hand-manipulated
leather tube built by Wolfgang von Kempelen in 1791, reproduced with
improvements by Sir Charles Wheatstone [140].
In electrical vocal-tract analog models, the piecewise
cylindrical acoustic tube is modeled as a cascade of electrical
transmission line segments, with each cylindrical segment being
modeled as a transmission line at some fixed characteristic impedance.
An early model employing four cylindrical sections was developed by
Hugh K. Dunn in the late 1940s [120]. An even earlier model
based on two cylinders joined by a conical section was published by
T. Chiba and M. Kajiyama in 1941 [120]. Cylinder
cross-sectional areas ![]() were determined based on X-ray images of
the vocal tract, and the corresponding characteristic impedances were
proportional to
were determined based on X-ray images of
the vocal tract, and the corresponding characteristic impedances were
proportional to ![]() . An impedance-based, lumped-parameter
approximation to the transmission-line sections was used in order that
analog LC ladders could be used to implement the model electronically.
By the 1950s, LC vocal-tract analog models included a side-branch for
nasal simulation [131].
. An impedance-based, lumped-parameter
approximation to the transmission-line sections was used in order that
analog LC ladders could be used to implement the model electronically.
By the 1950s, LC vocal-tract analog models included a side-branch for
nasal simulation [131].
The theory of transmission lines is credited to applied mathematician Oliver Heaviside (1850-1925), who worked out the telegrapher's equations (sometime after 1874) as an application of Maxwell's equations, which he simplified (sometime after 1880) from the original 20 equations of Maxwell to the modern vector formulation.A.12 Additionally, Heaviside is credited with introducing complex numbers into circuit analysis, inventing essentially Laplace-transform methods for solving circuits (sometime between 1880 and 1887), and coining the terms `impedance' (1886), `admittance' (1887), `electret', `conductance' (1885), and `permeability' (1885). A little later, Lord Rayleigh worked out the theory of waveguides (1897), including multiple propagating modes and the cut-off phenomenon.A.13
Singing Kelly-Lochbaum Vocal Tract
In 1962, John L. Kelly and Carol C. Lochbaum published a software version of a digitized vocal-tract analog model [245,246]. This may be the first instance of a sampled traveling-wave model of the vocal tract, as opposed to a lumped-parameter transmission-line model. In other words, Kelly and Lochbaum apparently returned to the original acoustic tube model (a sequence of cylinders), obtained d'Alembert's traveling-wave solution in each section, and applied Nyquist's sampling theorem to digitize the system. This sampled, bandlimited approach to digitization contrasts with the use of bilinear transforms as in wave digital filters; an advantage is that the frequency axis is not warped, but it is prone to aliasing when the parameters vary over time (or if nonlinearities are present).
At the junction of two cylindrical tube sections, i.e., at area discontinuities, lossless scattering occurs.A.14As mentioned in §A.5.4, reflection/transmission at impedance discontinuities was well formulated in classical network theory [34,35], and in transmission-line theory.
The Kelly-Lochbaum model can be regarded as a kind of ladder filter [297] or, more precisely, using later terminology, a digital waveguide filter [433]. Ladder and lattice digital filters can be used to realize arbitrary transfer functions [297], and they enjoy low sensitivity to round-off error, guaranteed stability under coefficient interpolation, and freedom from overflow oscillations and limit cycles under general conditions. Ladder/lattice filters remain important options when designing fixed-point implementations of digital filters, e.g., in VLSI. In the context of wave digital filters, the Kelly-Lochbaum model may be viewed as a digitized unit element filter [136], reminiscent of waveguide filters used in microwave engineering. In more recent terminology, it may be called a digital waveguide model of the vocal tract in which the digital waveguides are degenerated to single-sample width [433,442,452].
In 1961, Kelly and Lochbaum collaborated with Max Mathews to create what was most likely the first digital physical-modeling synthesis example by any method.A.15 The voice was computed on an IBM 704 computer using speech-vowel data from Gunnar Fant's recent book [132]. Interestingly, Fant's vocal-tract shape data were obtained (via x-rays) for Russian vowels, not English, but they were close enough to be understandable. Arthur C. Clarke, visiting John Pierce at Bell Labs, heard this demo, and he later used it in ``2001: A Space Odyssey,''--the HAL9000 computer slowly sang its ``first song'' (``Bicycle Built for Two'') as its disassembly by astronaut Dave Bowman neared completion.A.16
Perhaps due in part to J. L. Kelly's untimely death afterward, research on vocal-tract analog models tapered off thereafter, although there was some additional work [306]. Perhaps the main reason for the demise of this research thread was that spectral models (both nonparametric models such as the vocoder, and parametric source-filter models such as linear predictive coding (discussed below)) proved to be more effective when the application was simply speech coding at acceptably low bit rates and high fidelity levels. In telephone speech-coding applications, there was no requirement that a physical voice model be retained for purposes of expressive musical performance. In fact, it was desired to automate and minimize the ``performance expertise'' required to operate the voice production model. One could go so far as to say that the musical expressivity of voice synthesis models reached their peak in the 1939 Voder and related (manual) systems (§A.6.1).
In computer music, the Kelly-Lochbaum vocal tract model was revived for singing-voice synthesis in the thesis research of Perry Cook [87].A.17 In addition to the basic vocal tract model with side branch for the nasal tract, Cook included neck radiation (e.g., for `b'), and damping extensions. Additional work on incorporating damping within the tube sections was carried out by Amir et al. [15]. Other extensions include sparse acoustic tube modeling [149] and extension to piecewise conical acoustic tubes [507]. The digital waveguide modeling framework [430,431,433] can be viewed as an adaptation of extremely sparse acoustic-tube models for artificial reverberation, vibrating strings, and wind-instrument bores.
Linear Predictive Coding of Speech
Approximately a decade after the Kelly-Lochbaum voice model was developed, Linear Predictive Coding (LPC) of speech began [20,296,297]. The linear-prediction voice model is best classified as a parametric, spectral, source-filter model, in which the short-time spectrum is decomposed into a flat excitation spectrum multiplied by a smooth spectral envelope capturing primarily vocal formants (resonances).
LPC has been used quite often as a spectral transformation technique in computer music, as well as for general-purpose audio spectral envelopes [381], and it remains much used for low-bit-rate speech coding in the variant known as Codebook Excited Linear Prediction (CELP) [337].A.18When applying LPC to audio at high sampling rates, it is important to carry out some kind of auditory frequency warping, such as according to mel, Bark, or ERB frequency scales [182,459,482].
Interestingly, it was recognized from the beginning that the all-pole
LPC vocal-tract model could be interpreted as a modified
piecewise-cylindrical acoustic-tube model [20,297],
and this interpretation was most explicit when the vocal-tract filters
(computed by LPC in direct form) were realized as ladder filters
[297]. The physical interpretation is not really valid, however,
unless the vocal-tract filter parameters are estimated jointly with a
realistic glottal pulse shape.
LPC demands that the vocal
tract be driven by a flat spectrum--either an impulse (or
low-pitched impulse train) or white noise--which is not physically
accurate. When the glottal pulse shape (and lip radiation
characteristic) are ``factored out'', it becomes possible to convert
LPC coefficients into vocal-tract shape parameters (area ratios).
Approximate results can be obtained by assuming a simple roll-off
characteristic for the glottal pulse spectrum (e.g., -12 dB/octave) and
lip-radiation frequency response (nominally +6dB /octave), and
compensating with a simple preemphasis characteristic (e.g.,
![]() dB/octave) [297].
More accurate glottal pulse estimation in terms of parameters of the
derivative-glottal-wave models by Liljencrants, Fant, and Klatt
[133,257] (still assuming +6dB/octave for lip radiation)
was carried out in the thesis research of Vicky Lu
[290], and further extension of that work appears in
[250,213,251].
dB/octave) [297].
More accurate glottal pulse estimation in terms of parameters of the
derivative-glottal-wave models by Liljencrants, Fant, and Klatt
[133,257] (still assuming +6dB/octave for lip radiation)
was carried out in the thesis research of Vicky Lu
[290], and further extension of that work appears in
[250,213,251].
Formant Synthesis Models
A formant synthesizer is a source-filter model in which the source models the glottal pulse train and the filter models the formant resonances of the vocal tract. Constrained linear prediction can be used to estimate the parameters of formant synthesis models, but more generally, formant peak parameters may be estimated directly from the short-time spectrum (e.g., [255]). The filter in a formant synthesizer is typically implemented using cascade or parallel second-order filter sections, one per formant. Most modern rule-based text-to-speech systems descended from software based on this type of synthesis model [255,256,257].
Another type of formant-synthesis method, developed specifically for singing-voice synthesis is called the FOF method [386]. It can be considered an extension of the VOSIM voice synthesis algorithm [219]. In the FOF method, the formant filters are implemented in the time domain as parallel second-order sections; thus, the vocal-tract impulse response is modeled a sum of three or so exponentially decaying sinusoids. Instead of driving this filter with a glottal pulse wave, a simple impulse is used, thereby greatly reducing computational cost. A convolution of an impulse response with an impulse train is simply a periodic superposition of the impulse response. In the VOSIM algorithm, the impulse response was trimmed to one period in length, thereby avoiding overlap and further reducing computations.
The FOF method also tapers the beginning of the impulse-response using a rising half-cycle of a sinusoid. This qualitatively reduces the ``buzziness'' of the sound, and compensates for having replaced the glottal pulse with an impulse. In practice, however, the synthetic signal is matched to the desired signal in the frequency domain, and the details of the onset taper are adjusted to optimize audio quality more generally, including to broaden the formant resonances.
One of the difficulties of formant synthesis methods is that formant
parameter estimation is not always easy [408].
The problem is particularly difficult when the fundamental frequency
![]() is so high that the formants are not adequately ``sampled'' by
the harmonic frequencies, such as in high-pitched female voice
samples. Formant ambiguities due to insufficient spectral sampling
can often be resolved by incorporating additional physical constraints
to the extent they are known.
is so high that the formants are not adequately ``sampled'' by
the harmonic frequencies, such as in high-pitched female voice
samples. Formant ambiguities due to insufficient spectral sampling
can often be resolved by incorporating additional physical constraints
to the extent they are known.
Formant synthesis is an effective combination of physical and spectral modeling approaches. It is a physical model in that there is an explicit division between glottal-flow wave generation and the formant-resonance filter, despite the fact that a physical model is rarely used for either the glottal waveform or the formant resonator. On the other hand, it is a spectral modeling method in that its parameters are estimated by explicitly matching short-time audio spectra of desired sounds. It is usually most effective for any synthesis model, physical or otherwise, to be optimized in the ``audio perception'' domain to the extent it is known how to do this [312,165]. For an illustrative example, see, e.g., [201].
Further Reading in Speech Synthesis
More on the history and practice of speech synthesis can be found in, e.g., [139,140,142,408,335,106]. A surprisingly complete collection of sound examples spanning the history of speech synthesis can be heard on the CD-ROM accompanying a JASA-87 review article by Dennis Klatt [256]. Sound examples of these and related models in music applications may be found online as well [448].
String Models
As mentioned in §A.5.2, the first known computational models of vibrating strings were based on finite difference modeling by Ruiz and Hiller [194]. In the field of musical acoustics, software simulations of bowed strings were being carried out by Michael E. McIntyre and James Woodhouse as early as the mid 1970s [307]. In these simulations, the string is represented by the ``Green's function'' (impulse response) seen by a traveling wave traversing the string once in both directions (i.e., one round trip). This model was evidently based on investigations in the 1960s by John Schelleng, Lothar Cremer, and Cremer's co-worker Hans Lazarus into the behavior of the so-called ``corner rounding function'' (round-trip impulse response) in the context of bowed-string dynamics [409,410,95].A.19 The bow-string junction was based on theory worked out by Friedlander [151] and Keller [244], both published in 1953. These mathematical models of bowed-string dynamics were in turn preceded by influential investigations by Raman, published in 1918 [365], and Hermann von Helmholtz, published in 1863 [538]. An important enabling scientific measurement was that of the friction curve describing the bow-string contact, and many models, such as in [307,308] used a hyperbolic friction curve, approximating measurements by Lazarus [95]. Interestingly, while researchers in musical acoustics would often use their models to produce example waveforms illustrating the successful modeling of various visible physical effects, they apparently never listened to them as sound.
Robert T. Schumacher, who had been interested primarily in woodwind musical acoustics, collaborated with McIntyre and Woodhouse, and the result was a generalization of the Friedlander-Keller bowed-string model to wind instruments [308].
Incidentally, electrical equivalent circuits for bowed-string instruments appeared as early as 1952 [332, p. 122], with perhaps the most cited model being Schelleng's published in 1963 [409].
Karplus-Strong Algorithms
In 1983 the Karplus-Strong [236] and Extended Karplus-Strong
(EKS) [207,428] algorithms were published (in the
same issue of the Computer Music Journal). Kevin Karplus and Alex
Strong were computer science students at Stanford trying out wavetable
synthesis algorithms on an 8-bit microcomputer. The sounds were
rather boring, as any precisely periodic sound tends to be, so Strong
had the idea of filtering the wavetable by a two-point average,
![]() ,
on each reading pass (which requires no multiplies), in order to
change the timbre dynamically. The result sounded curiously like a
string, almost no matter what initial table was used. After some
experimentation, they settled on random numbers as the standard
excitation. Strong played in a string quartet with David Jaffe, a
CCRMA Composition PhD student, and Jaffe decided to use the algorithm
in his piece ``Silicon Valley Breakdown'' (1982) which became a tour
de force demonstration of the EKS algorithm. In preparation for the
piece, Jaffe approached the author regarding how to obtain better
musical control over tuning, brightness, dynamic level, and the like,
and the resulting extensions were described in
[207,428]. Having studied the McIntyre-Woodhouse
papers, the author recognized the filtered-delay-loop in the
Karplus-Strong algorithm as having the same transfer function as that
of an idealized vibrating string [428]. This equivalence later
led to deriving the Karplus-Strong algorithm as a special case of a
digital waveguide string model (see Chapter 6 up to
§9.1.4 for the derivation). When viewed as a digital waveguide
model, the musical quality and expressivity of the EKS algorithm
suggested (ca. 1985) that extremely simplified traveling-wave models
with sparsely lumped losses and dispersion could capture the necessary
dimensions of musical expressivity at very low computational cost.
,
on each reading pass (which requires no multiplies), in order to
change the timbre dynamically. The result sounded curiously like a
string, almost no matter what initial table was used. After some
experimentation, they settled on random numbers as the standard
excitation. Strong played in a string quartet with David Jaffe, a
CCRMA Composition PhD student, and Jaffe decided to use the algorithm
in his piece ``Silicon Valley Breakdown'' (1982) which became a tour
de force demonstration of the EKS algorithm. In preparation for the
piece, Jaffe approached the author regarding how to obtain better
musical control over tuning, brightness, dynamic level, and the like,
and the resulting extensions were described in
[207,428]. Having studied the McIntyre-Woodhouse
papers, the author recognized the filtered-delay-loop in the
Karplus-Strong algorithm as having the same transfer function as that
of an idealized vibrating string [428]. This equivalence later
led to deriving the Karplus-Strong algorithm as a special case of a
digital waveguide string model (see Chapter 6 up to
§9.1.4 for the derivation). When viewed as a digital waveguide
model, the musical quality and expressivity of the EKS algorithm
suggested (ca. 1985) that extremely simplified traveling-wave models
with sparsely lumped losses and dispersion could capture the necessary
dimensions of musical expressivity at very low computational cost.
Digital Waveguide Models
The digital waveguide modeling paradigm was developed in 1985-86 as a guaranteed-stable ``construction kit'' for lossless reverberator prototypes supporting general feedback topologies [430]. The following year, digital waveguide building blocks were extended to vibrating strings and single-cylinder acoustic tubes (principally for the clarinet family) [431]. A modular synthesis architecture was developed in which various ``nonlinear junctions'' could be used to excite digital waveguide networks of general design. The iterative Friedlander-Keller solver of [308] was replaced by a look-up table plus a couple of additions and a multiply, facilitating sound synthesis in real time. This computational model was presented, with sound examples, at the 1986 ICMC, and it so happened that Yamaha's chief engineer was in the audience. Perhaps significantly, the FM synthesis patent was nearing the end of its life. Yamaha soon hired some consultants to evaluate waveguide synthesis, and in 1989 they began a strenuous development effort culminating in the VL1 (``Virtual Lead'') synthesizer family, introduced in the U.S. at the 1994 NAMM show in LA. The jazz trio demonstrating the VL1 at NAMM created quite a ``buzz'', and the cover of Keyboard Magazine soon proclaimed it as ``The Next Big Thing'' in synthesis technology [375]. As it happened, physical modeling synthesis did not immediately meet with large commercial success, perhaps because wavetable synthesis required less computation and was so much easier to ``voice'', and because memory was fairly inexpensive. The market at large simply has not yet demanded more expressive sound synthesis algorithms than what wavetable synthesis can provide. However, the quality of the VL1 in the hands of skilled players constituted proof-of-concept for many of us, and helped stimulate further academic interest in the approach. Trained performing musicians generally prefer the expressive richness of a computational physical model, and find wavetable synthesis to be comparatively limiting, as typically implemented.
Summary
This appendix has attempted to trace some of the early technical developments which enabled and shaped virtual acoustic musical instrument technology as addressed in this book, particularly for the case of virtual stringed instruments. For the early period covered (roughly up to the mid 1980s), many lines of developments specifically in the fields of acoustics and musical acoustics per se have been omitted. Some recent review articles include [445,515]. For sound examples and few other recent developments, see the companion overheads for this appendix [448].
Next Section:
Elementary Physics, Mechanics, and Acoustics
Previous Section:
Conclusion