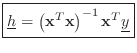Free Books
   Free Books    Introduction to Digital Filters  

Matrix Filter Representations

This appendix introduces various matrix representations for digital filters, including the important state space formulation. Additionally, elementary system identification based on a matrix description is described.


Introduction

It is illuminating to look at matrix representations of digital filters.F.1Every linear digital filter can be expressed as a constant matrix $ \mathbf{h}$ multiplying the input signal $ {\underline{x}}$ (the input vector) to produce the output signal (vector) $ \underline{y}$, i.e.,

$\displaystyle \underline{y}= \mathbf{h}{\underline{x}}. $

For simplicity (in this appendix only), we will restrict attention to finite-length inputs $ {\underline{x}}^T = [x_0,\ldots,x_{N-1}]$ (to avoid infinite matrices), and the output signal will also be length $ N$. Thus, the filter matrix $ \mathbf{h}$ is a square $ N\times N$ matrix, and the input/output signal vectors are $ N\times 1$ column vectors.

More generally, any finite-order linear operator can be expressed as a matrix multiply. For example, the Discrete Fourier Transform (DFT) can be represented by the ``DFT matrix'' $ [e^{-j2\pi kn/N}]$, where the column index $ n$ and row index $ k$ range from 0 to $ N-1$ [84, p. 111].F.2Even infinite-order linear operators are often thought of as matrices having infinite extent. In summary, if a digital filter is linear, it can be represented by a matrix.

General Causal Linear Filter Matrix

To be causal, the filter output at time $ n\in[0,N-1]$ cannot depend on the input at any times $ m$ greater than $ n$. This implies that a causal filter matrix must be lower triangular. That is, it must have zeros above the main diagonal. Thus, a causal linear filter matrix $ \mathbf{h}$ will have entries that satisfy $ h_{mn}=0$ for $ n>m$.

For example, the general $ 3\times 3$ causal, linear, digital-filter matrix operating on three-sample sequences is

$\displaystyle \mathbf{h}= \left[\begin{array}{ccc} h_{00} & 0 & 0\\ [2pt] h_{10} & h_{11} & 0\\ [2pt] h_{20} & h_{21} & h_{22} \end{array}\right] $

and the input-output relationship is of course

$\displaystyle \left[\begin{array}{c} y_0 \\ [2pt] y_1 \\ [2pt] y_2\end{array}\r... ...left[\begin{array}{c} x_0 \\ [2pt] x_1 \\ [2pt] x_2\end{array}\right], \protect$ (F.1)

or, more explicitly,
$\displaystyle y_0$ $\displaystyle =$ $\displaystyle h_{00} x_0$  
$\displaystyle y_1$ $\displaystyle =$ $\displaystyle h_{10} x_0 + h_{11}x_1$  
$\displaystyle y_2$ $\displaystyle =$ $\displaystyle h_{20} x_0 + h_{21}x_1 + h_{22} x_2. \protect$ (F.2)

While Eq.$ \,$(F.2) covers the general case of linear, causal, digital filters operating on the space of three-sample sequences, it includes time varying filters, in general. For example, the gain of the ``current input sample'' changes over time as $ h_{00}, h_{11}, h_{22}$.

General LTI Filter Matrix

The general linear, time-invariant (LTI) matrix is Toeplitz. A Toeplitz matrix is constant along all its diagonals. For example, the general $ 3\times 3$ LTI matrix is given by

$\displaystyle \mathbf{h}= \left[\begin{array}{ccc} h_{0} & h_{-1} & h_{-2}\\ [2pt] h_{1} & h_{0} & h_{-1}\\ [2pt] h_{2} & h_{1} & h_{0} \end{array}\right] $

and restricting to causal LTI filters yields

$\displaystyle \mathbf{h}= \left[\begin{array}{ccc} h_{0} & 0 & 0\\ [2pt] h_{1} & h_{0} & 0\\ [2pt] h_{2} & h_{1} & h_{0} \end{array}\right]. $

Note that the gain of the ``current input sample'' is now fixed at $ h_0$ for all time. Also note that we can handle only length 3 FIR filters in this representation, and that the output signal is ``cut off'' at time $ n=3$. The cut-off time is one sample after the filter is fully ``engaged'' by the input signal (all filter coefficients see data). Even if the input signal is zero at time $ n=3$ and beyond, the filter should be allowed to ``ring'' for another two samples. We can accommodate this by appending two zeros to the input and going with a $ 5\times 5$ banded Toeplitz filter matrix:

$\displaystyle \left[\begin{array}{c} y_0 \\ [2pt] y_1 \\ [2pt] y_2 \\ [2pt] y_3... ...{array}{c} x_0 \\ [2pt] x_1 \\ [2pt] x_2 \\ [2pt] 0\\ [2pt] 0\end{array}\right]$ (F.3)

We could add more rows to obtain more output samples, but the additional outputs would all be zero.

In general, if a causal FIR filter is length $ N_h$, then its order is $ N_h-1$, so to avoid ``cutting off'' the output signal prematurely, we must append at least $ N_h-1$ zeros to the input signal. Appending zeros in this way is often called zero padding, and it is used extensively in spectrum analysis [84]. As a specific example, an order 5 causal FIR filter (length 6) requires 5 samples of zero-padding on the input signal to avoid output truncation.

If the FIR filter is noncausal, then zero-padding is needed before the input signal in order not to ``cut off'' the ``pre-ring'' of the filter (the response before time $ n = 0$).

To handle arbitrary-length input signals, keeping the filter length at 3 (an order 2 FIR filter), we may simply use a longer banded Toeplitz filter matrix:

$\displaystyle \mathbf{h}= \left[\begin{array}{ccccccc} h_0 & 0 & 0 & 0 & 0 & 0... ...& \\ \vdots & \vdots & \vdots & & \ddots & \ddots & \ddots \end{array}\right] $

A complete matrix representation of an LTI digital filter (allowing for infinitely long input/output signals) requires an infinite Toeplitx matrix, as indicated above. Instead of working with infinite matrices, however, it is more customary to speak in terms of linear operators [56]. Thus, we may say that every LTI filter corresponds to a Toeplitz linear operator.

Cyclic Convolution Matrix

An infinite Toeplitz matrix implements, in principle, acyclic convolution (which is what we normally mean when we just say ``convolution''). In practice, the convolution of a signal $ x$ and an impulse response $ h$, in which both $ x$ and $ h$ are more than a hundred or so samples long, is typically implemented fastest using FFT convolution (i.e., performing fast convolution using the Fast Fourier Transform (FFT) [84]F.3). However, the FFT computes cyclic convolution unless sufficient zero padding is used [84]. The matrix representation of cyclic (or ``circular'') convolution is a circulant matrix, e.g.,

$\displaystyle \mathbf{h}= \left[\begin{array}{cccccc} h_0 & 0 & 0 & 0 & h_2 & ... ... h_2 & h_1 & h_0 & 0 \\ [2pt] 0 & 0 & 0 & h_2 & h_1 & h_0 \end{array}\right]. $

As in this example, each row of a circulant matrix is obtained from the previous row by a circular right-shift. Circulant matrices are thus always Toeplitz (but not vice versa). Circulant matrices have many interesting properties.F.4 For example, the eigenvectors of an $ N\times N$ circulant matrix are the DFT sinusoids for a length $ N$ DFT [84]. Similarly, the eigenvalues may be found by simply taking the DFT of the first row.

The DFT eigenstructure of circulant matrices is directly related to the DFT convolution theorem [84]. The above $ 6\times 6$ circulant matrix $ \mathbf{h}$, when multiplied times a length 6 vector $ {\underline{x}}$, implements cyclic convolution of $ {\underline{x}}$ with $ \underline{h}=[h_0,h_1,h_3,0,0,0]$. Using the DFT to perform the circular convolution can be expressed as

$\displaystyle \underline{y}={\underline{x}}\circledast \underline{h}=$IDFT$\displaystyle ($DFT$\displaystyle ({\underline{x}})\cdot$DFT$\displaystyle (\underline{h})), $

where ` $ \circledast $' denotes circular convolution. Let $ \mathbf{S}$ denote the matrix of sampled DFT sinusoids for a length $ N$ DFT: $ \mathbf{S}[k,n]\isdeftext e^{j2\pi k n/N}$. Then $ \mathbf{S}^\ast$ is the DFT matrix, where `$ \ast $' denotes Hermitian transposition (transposition and complex-conjugation). The DFT of the length-$ N$ vector $ {\underline{x}}$ can be written as $ \underline{X}=\mathbf{S}^\ast\,{\underline{x}}$, and the corresponding inverse DFT is $ {\underline{x}}=(1/N)\mathbf{S}\underline{X}$. The DFT-eigenstructure of circulant matrices provides that a real $ N\times N$ circulant matrix $ \mathbf{h}$ having top row $ \underline{h}^T$ satisfies $ \mathbf{h}\mathbf{S}= \mathbf{S}\cdot$   diag$ (\underline{H})$, where $ \underline{H}=\mathbf{S}^\ast\,\underline{h}$ is the length $ N$ DFT of $ \underline{h}$, and diag$ (\underline{H})$ denotes a diagonal matrix with the elements of $ \underline{H}$ along the diagonal. Therefore, diag$ (\underline{H})=\mathbf{S}^{-1}\mathbf{h}\mathbf{S}=(1/N)\mathbf{S}^\ast\,\mathbf{h}\,\mathbf{S}$. By the DFT convolution theorem,

\begin{eqnarray*} \underline{y}=\underline{h}\circledast {\underline{x}} &\Leftr... ...{X}=(1/N)\mathbf{S}^\ast\,\mathbf{h}\,\mathbf{S}\,\underline{X}. \end{eqnarray*}

Premultiplying by the IDFT matrix $ (1/N)\mathbf{S}$ yields

$\displaystyle \underline{y}= (1/N)\mathbf{S}\underline{Y}=(1/N)\mathbf{S}\mathbf{S}^\ast\,\mathbf{h}\,(1/N)\mathbf{S}\underline{X}= \mathbf{h}{\underline{x}}. $

Thus, the DFT convolution theorem holds if and only if the circulant convolution matrix $ \mathbf{h}$ has eigenvalues $ \underline{H}$ and eigenvectors given by the columns of $ \mathbf{S}$ (the DFT sinusoids).

Inverse Filters

Note that the filter matrix $ \mathbf{h}$ is often invertible [58]. In that case, we can effectively run the filter backwards:

$\displaystyle {\underline{x}}= \mathbf{h}^{-1} \underline{y} $

However, an invertible filter matrix does not necessarily correspond to a stable inverse-filter when the lengths of the input and output vectors are allowed to grow larger. For example, the inverted filter matrix may contain truncated growing exponentials, as illustrated in the following matlab example:
> h = toeplitz([1,2,0,0,0],[1,0,0,0,0])
h =
  1  0  0  0  0
  2  1  0  0  0
  0  2  1  0  0
  0  0  2  1  0
  0  0  0  2  1
> inv(h)
ans =
    1    0    0    0    0
   -2    1    0    0    0
    4   -2    1    0    0
   -8    4   -2    1    0
   16   -8    4   -2    1
The inverse of the FIR filter $ h=[1,2]$ is in fact unstable, having impulse response $ h_i(n)=(-2)^n$, $ n=0,1,2,\ldots\,$, which grows to $ \infty$ with $ n$.

Another point to notice is that the inverse of a banded Toeplitz matrix is not banded (although the inverse of lower-triangular [causal] matrix remains lower triangular). This corresponds to the fact that the inverse of an FIR filter is an IIR filter.

State Space Realization

Above, we used a matrix multiply to represent convolution of the filter input signal with the filter's impulse response. This only works for FIR filters since an IIR filter would require an infinite impulse-response matrix. IIR filters have an extensively used matrix representation called state space form (or ``state space realizations''). They are especially convenient for representing filters with multiple inputs and multiple outputs (MIMO filters). An order $ N$ digital filter with $ p$ inputs and $ q$ outputs can be written in state-space form as follows:

$\displaystyle {\underline{x}}(n+1)$ $\displaystyle =$ $\displaystyle A {\underline{x}}(n) + B \underline{u}(n)$  
$\displaystyle \underline{y}(n)$ $\displaystyle =$ $\displaystyle C {\underline{x}}(n) + D\underline{u}(n) \protect$ (F.4)

where $ {\underline{x}}(n)$ is the length $ N$ state vector at discrete time $ n$, $ \underline{u}(n)$ is a $ p\times 1$ vector of inputs, and $ \underline{y}(n)$ the $ q\times 1$ output vector. $ A$ is the $ N\times N$ state transition matrix, and it determines the dynamics of the system (its poles, or resonant modes).

State-space models are described further in Appendix G. Here, we will only give an illustrative example and make a few observations:

State Space Filter Realization Example

The digital filter having difference equation

$\displaystyle y(n) = u(n-1) + u(n-2) + 0.5\, y(n-1) - 0.1\, y(n-2) + 0.01\, y(n-3) $

can be realized in state-space form as follows:F.5
$\displaystyle \left[\begin{array}{c} x_1(n+1) \\ [2pt] x_2(n+1) \\ [2pt] x_3(n+1)\end{array}\right]$ $\displaystyle =$ $\displaystyle \left[\begin{array}{ccc} 0 & 1 & 0\\ [2pt] 0 & 0 & 1\\ [2pt] 0.01... ...\right] + \left[\begin{array}{c} 0 \\ [2pt] 0 \\ [2pt] 1\end{array}\right] u(n)$  
$\displaystyle \underline{y}(n)$ $\displaystyle =$ $\displaystyle \left[\begin{array}{ccc} 0 & 1 & 1\end{array}\right] \left[\begin{array}{c} x_1(n) \\ [2pt] x_2(n) \\ [2pt] x_3(n)\end{array}\right] \protect$ (F.5)

Thus, $ {\underline{x}}(n) = [x_1(n), x_2(n), x_3(n)]^T$ is the vector of state variables at time $ n$, $ B = [0,0,1]^T$ is the state-input gain vector, $ C = [0,1,1]$ is the vector of state-gains for the output, and the direct-path gain is $ D=0$.

This example is repeated using matlab in §G.7.8 (after we have covered transfer functions).

A general procedure for converting any difference equation to state-space form is described in §G.7. The particular state-space model shown in Eq.$ \,$(F.5) happens to be called controller canonical form, for reasons discussed in Appendix G. The set of all state-space realizations of this filter is given by exploring the set of all similarity transformations applied to any particular realization, such as the control-canonical form in Eq.$ \,$(F.5). Similarity transformations are discussed in §G.8, and in books on linear algebra [58].

Note that the state-space model replaces an $ N$th-order difference equation by a vector first-order difference equation. This provides elegant simplifications in the theory and analysis of digital filters. For example, consider the case $ B=C=I$, and $ D=0$, so that Eq.$ \,$(F.4) reduces to

$\displaystyle \underline{y}(n+1) = A \underline{y}(n) + \underline{u}(n), \protect$ (F.6)

where $ A$ is the $ N\times N$ transition matrix, and both $ \underline{u}(n)$ and $ \underline{y}(n)$ are $ N\times 1$ signal vectors. (This filter has $ N$ inputs and $ N$ outputs.) This vector first-order difference equation is analogous to the following scalar first-order difference equation:

$\displaystyle y(n+1) = a y(n) + u(n) $

The response of this filter to its initial state $ y(0)$ is given by

$\displaystyle y(n) = a^n y(0), \quad n=0,1,2,3,\ldots\,. $

(This is the zero-input response of the filter, i.e., $ u(n)\equiv 0$.) Similarly, setting $ \underline{u}(n)=0$ to in Eq.$ \,$(F.6) yields

$\displaystyle \underline{y}(n) = A^n \underline{y}(0), \quad n=0,1,2,3,\ldots\,. $

Thus, an $ N$th-order digital filter ``looks like'' a first-order digital filter when cast in state-space form.

Time Domain Filter Estimation

System identification is the subject of identifying filter coefficients given measurements of the input and output signals [46,78]. For example, one application is amplifier modeling, in which we measure (1) the normal output of an electric guitar (provided by the pick-ups), and (2) the output of a microphone placed in front of the amplifier we wish to model. The guitar may be played in a variety of ways to create a collection of input/output data to use in identifying a model of the amplifier's ``sound.'' There are many commercial products which offer ``virtual amplifier'' presets developed partly in such a way.F.6 One can similarly model electric guitars themselves by measuring the pick signal delivered to the string (as the input) and the normal pick-up-mix output signal. A separate identification is needed for each switch and tone-control position. After identifying a sampling of models, ways can be found to interpolate among the sampled settings, thereby providing ``virtual'' tone-control knobs that respond like the real ones [101].

In the notation of the §F.1, assume we know $ {\underline{x}}$ and $ \underline{y}$ and wish to solve for the filter impulse response $ \underline{h}^T=[h_0,h_1,\ldots,h_{N_h-1}]$. We now outline a simple yet practical method for doing this, which follows readily from the discussion of the previous section.

Recall that convolution is commutative. In terms of the matrix representation of §F.3, this implies that the input signal and the filter can switch places to give

$\displaystyle \underbrace{% \left[\begin{array}{c} y_0 \\ [2pt] y_1 \\ [2pt] y... ... h_2 \\ [2pt] h_3\\ [2pt] h_4\end{array}\right]}_{\displaystyle\underline{h}}, $

or

$\displaystyle \underline{y}= \mathbf{x}\underline{h}. \protect$ (F.7)

Here we have indicated the general case for a length $ N_h=5$ causal FIR filter, with input and output signals that go on forever. While $ \mathbf{x}$ is not invertible because it is not square, we can solve for $ \underline{h}$ under general conditions by taking the pseudoinverse of $ \mathbf{x}$. Doing this provides a least-squares system identification method [46].

The Moore-Penrose pseudoinverse is easy to derive.F.7 First multiply Eq.$ \,$(F.7) on the left by the transpose of $ \mathbf{x}$ in order to obtain a ``square'' system of equations:

$\displaystyle \mathbf{x}^T\underline{y}= \mathbf{x}^T\mathbf{x}\underline{h} $

Since $ \mathbf{x}^T\mathbf{x}$ is a square $ N_h\times N_h$ matrix, it is invertible under general conditions, and we obtain the following formula for $ \underline{h}$:

$\displaystyle \zbox {\underline{h}= \left(\mathbf{x}^T\mathbf{x}\right)^{-1}\mathbf{x}^T\underline{y}} \protect$ (F.8)

Thus, $ \left(\mathbf{x}^T\mathbf{x}\right)^{-1}\mathbf{x}^T$ is the Moore-Penrose pseudoinverse of $ \mathbf{x}$.

If the input signal $ x$ is an impulse $ \delta (n)$ (a 1 at time zero and 0 at all other times), then $ \mathbf{x}^T\mathbf{x}$ is simply the identity matrix, which is its own inverse, and we obtain $ \underline{h}=\underline{y}$. We expect this by definition of the impulse response. More generally, $ \mathbf{x}^T\mathbf{x}$ is invertible whenever the input signal is ``sufficiently exciting'' at all frequencies. An LTI filter frequency response can be identified only at frequencies that are excited by the input, and the accuracy of the estimate at any given frequency can be improved by increasing the input signal power at that frequency. [46].

Effect of Measurement Noise

In practice, measurements are never perfect. Let $ \hat{\underline{y}}=\underline{y}+\underline{e}$ denote the measured output signal, where $ \underline{e}$ is a vector of ``measurement noise'' samples. Then we have

$\displaystyle \hat{\underline{y}}= \underline{y}+ \underline{e}= \mathbf{x}\underline{h}+ \underline{e}. $

By the orthogonality principle [38], the least-squares estimate of $ \underline{h}$ is obtained by orthogonally projecting $ \hat{\underline{y}}$ onto the space spanned by the columns of $ \mathbf{x}$. Geometrically speaking, choosing $ \underline{h}$ to minimize the Euclidean distance between $ \hat{\underline{y}}$ and $ \mathbf{x}\underline{h}$ is the same thing as choosing it to minimize the sum of squared estimated measurement errors $ \vert\vert\,\underline{e}\,\vert\vert ^2$. The distance from $ \mathbf{x}\underline{h}$ to $ \hat{\underline{y}}$ is minimized when the projection error $ \underline{e}=\hat{\underline{y}}-\mathbf{x}\underline{h}$ is orthogonal to every column of $ \mathbf{x}$, which is true if and only if $ \mathbf{x}^T\underline{e}=0$ [84]. Thus, we have, applying the orthogonality principle,

$\displaystyle 0 = \mathbf{x}^T\underline{e}= \mathbf{x}^T(\underline{y}- \mathb... ...nderline{h}) = \mathbf{x}^T\underline{y}- \mathbf{x}^T\mathbf{x}\underline{h}. $

Solving for $ \underline{h}$ yields Eq.$ \,$(F.8) as before, but this time we have derived it as the least squares estimate of $ \underline{h}$ in the presence of output measurement error.

It is also straightforward to introduce a weighting function in the least-squares estimate for $ \underline{h}$ by replacing $ \mathbf{x}^T$ in the derivations above by $ \mathbf{x}^TR$, where $ R$ is any positive definite matrix (often taken to be diagonal and positive). In the present time-domain formulation, it is difficult to choose a weighting function that corresponds well to audio perception. Therefore, in audio applications, frequency-domain formulations are generally more powerful for linear-time-invariant system identification. A practical example is the frequency-domain equation-error method described in §I.4.4 [78].

Matlab System Identification Example

The Octave output for the following small matlab example is listed in Fig.F.1:

delete('sid.log'); diary('sid.log'); % Log session
echo('on');       % Show commands as well as responses
N = 4;            % Input signal length
%x = rand(N,1)    % Random input signal - snapshot:
x = [0.056961, 0.081938, 0.063272, 0.672761]'
h = [1 2 3]';     % FIR filter
y = filter(h,1,x) % Filter output
xb = toeplitz(x,[x(1),zeros(1,N-1)]) % Input matrix
hhat = inv(xb' * xb) * xb' * y % Least squares estimate
% hhat = pinv(xb) * y % Numerically robust pseudoinverse
hhat2 = xb\y % Numerically superior (and faster) estimate
diary('off'); % Close log file
One fine point is the use of the syntax `` $ \underline{h}= \mathbf{x}\backslash\underline{y}$'', which has been a matlab language feature from the very beginning [82]. It is usually more accurate (and faster) than multiplying by the explicit pseudoinverse. It uses the QR decomposition to convert the system of linear equations into upper-triangular form (typically using Householder reflections), determine the effective rank of $ \mathbf{x}$, and backsolve the reduced triangular system (starting at the bottom, which goes very fast) [29, §6.2].F.8

Figure F.1: Time-domain system-identification matlab example.
  
+ echo('on');       % Show commands as well as responses
+ N = 4;            % Input signal length
+ %x = rand(N,1)    % Random input signal - snapshot:
+ x = [0.056961, 0.081938, 0.063272, 0.672761]'
x =
  0.056961
  0.081938
  0.063272
  0.672761

+ h = [1 2 3]';     % FIR filter
+ y = filter(h,1,x) % Filter output
y =
  0.056961
  0.195860
  0.398031
  1.045119

+ xb = toeplitz(x,[x(1),zeros(1,N-1)]) % Input matrix
xb =
  0.05696  0.00000  0.00000  0.00000
  0.08194  0.05696  0.00000  0.00000
  0.06327  0.08194  0.05696  0.00000
  0.67276  0.06327  0.08194  0.05696

+ hhat = inv(xb' * xb) * xb' * y % Least squares estimate
hhat =
   1.0000
   2.0000
   3.0000
   3.7060e-13

+ % hhat = pinv(xb) * y % Numerically robust pseudoinverse
+ hhat2 = xb\y % Numerically superior (and faster) estimate
hhat2 =
   1.0000
   2.0000
   3.0000
   3.6492e-16
Next Section:
State Space Filters
Previous Section:
Analog Filters