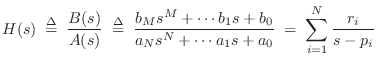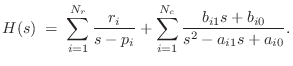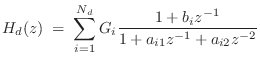DSPRelated.com
Free Books
   Free Books    Physical Audio Signal Processing  

Modal Expansion

A well known approach to transfer-function modeling is called modal synthesis, introduced in §1.3.9 [5,299,6,145,381,30]. Modal synthesis may be defined as constructing a source-filter synthesis model in which the filter transfer function is implemented as a sum of first- and/or second-order filter sections (i.e., as a parallel filter bank in which each filter is at most second-order--this was reviewed in §1.3.9). In other words, the physical system is represented as a superposition of individual modes driven by some external excitation (such as a pluck or strike).

In acoustics, the term mode of vibration, or normal mode, normally refers to a single-frequency spatial eigensolution of the governing wave equation. For example, the modes of an ideal vibrating string are the harmonically related sinusoidal string-shapes having an integer number of uniformly spaced zero-crossings (or nodes) along the string, including its endpoints. As first noted by Daniel Bernoulli (§A.2), acoustic vibration can be expressed as a superposition of component sinusoidal vibrations, i.e., as a superposition of modes.9.6

When a single mode is excited by a sinusoidal driving force, all points of the physical object vibrate at the same temporal frequency (cycles per second), and the mode shape becomes proportional to the spatial amplitude envelope of the vibration. The sound emitted from the top plate of a guitar, for example, can be represented as a weighted sum of the radiation patterns of the respective modes of the top plate, where the weighting function is constructed according to how much each mode is excited (typically by the guitar bridge) [143,390,109,205,209].

The impulse-invariant method (§8.2), can be considered a special case of modal synthesis in which a continuous-time $ s$-plane transfer function is given as a starting point. More typically, modal synthesis starts with a measured frequency response, and a second-order parallel filter bank is fit to that in some way. In particular, any filter-design technique may be used (§8.6), followed by a conversion to second-order parallel form.

Modal expansions find extensive application in industry for determining parametric frequency responses (superpositions of second-order modes) from measured vibration data [299]. Each mode is typically parametrized in terms of its resonant frequency, bandwidth (or damping), and gain (most generally complex gain, to include phase).

Modal synthesis can also be seen as a special case of source-filter synthesis, which may be defined as any signal model based on factoring a sound-generating process into a filter driven by some (usually relatively simple) excitation signal. An early example of source-filter synthesis is the vocoder (§A.6.1). Whenever the filter in a source-filter model is implemented as a parallel second-order filter bank, we can call it modal synthesis (although, strictly speaking, each filter section should correspond to a resonant mode of the modeled resonant system).

Also related to modal synthesis is so-called formant synthesis, used extensively in speech synthesis [219,255,389,40,81,491,490,313,363,297]. A formant is simply a filter resonance having some center-frequency, bandwidth, and (sometimes specified) gain. Thus, a formant corresponds to a single mode of vibration in the vocal tract. Many text-to-speech systems in use today are based on the Klatt formant synthesizer for speech [255].

Since the importance of spectral formants in sound synthesis has more to do with the way we hear than with the physical parameters of a system, formant synthesis is probably best viewed as a spectral modeling synthesis method [456], as opposed to a physical modeling technique [435]. An exception to this rule may occur when the system consists physically of a parallel bank of second-order resonators, such as an array of tuning forks or Helmholtz resonators. In such a case, the mode parameters correspond to physically independent objects; this is of course rare in practice.

In the linear, time-invariant case, only modes in the range of human hearing need to be retained in the model. Also, any ``uncontrollable'' or ``unobservable'' modes should obviously be left out as well. With these simplificiation, the modal representation is generally more efficient than an explicit mass-spring-dashpot digitization (§7.3). On the other hand, since the modal representation is usually not directly physical, nonlinear extensions may be difficult and/or behave unnaturally.

As in the impulse-invariant method (§8.2), starting with an order $ N$ transfer function $ H(s)$ describing the input-output behavior of a physical system, a modal description can be obtained immediately from the partial fraction expansion (PFE):

$\displaystyle H(s) \isdefs \frac{B(s)}{A(s)} \isdefs \frac{b_M s^M + \cdots b_1... ..._0}{a_N s^N + \cdots a_1 s + a_0} \eqsp \sum_{i=1}^N \frac{r_i}{s-p_i} \protect$ (9.9)

where $ p_i$ denotes the $ i$th pole, $ \xi_i$ is the $ i$th zero, and $ r_i$ is the residue of the $ i$th pole [449]. (For simplicity of notation, Eq.$ \,$(8.9) is written for the case $ M<N$ and $ p_i$ distinct. See [449] for the details when this is not the case.) Since the system is real, complex poles will occur in complex conjugate pairs. This means that for each complex term $ r_i/(s-p_i)$, the PFE will also include the complex-conjugate term $ \overline{r}_i/(s-\overline{p}_i)$. Such terms can be summed to create half as many real second-order terms:

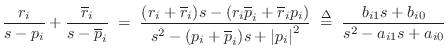$\displaystyle \frac{r_i}{s-p_i} + \frac{\overline{r}_i}{s-\overline{p}_i} \eqsp... ...vert p_i\right\vert^2} \isdefs \frac{b_{i1} s + b_{i0}}{s^2 - a_{i1}s + a_{i0}}$ (9.10)

Let $ N_c$ denote the number of complex pole pairs, and $ N_r = N-2N_c$ be the number of real poles. Then the modal expansion can be written as

$\displaystyle H(s) \eqsp \sum_{i=1}^{N_r} \frac{r_i}{s-p_i} + \sum_{i=1}^{N_c} \frac{b_{i1} s + b_{i0}}{s^2 - a_{i1}s + a_{i0}}. \protect$ (9.11)

The real poles, if any, can be paired off into a sum of second-order sections as well, with one first-order section left over when $ N_r$ is odd. Note that each component second-order mode consists of one zero and two poles. The zero is necessary to adjust the phase of the resonant mode. The mode phase affects the frequency response at frequencies between resonances (from smoothly varying to the appearance of a deep notch somewhere between them).

A typical practical implementation of each mode in the sum is by means of second-order filter, or biquad section [449]. A biquad section is easily converted from continuous- to discrete-time form, such as by the impulse-invariant method of §8.2. The final discrete-time model then consist of a parallel bank of second-order digital filters

$\displaystyle H_d(z) \eqsp \sum_{i=1}^{N_d} G_i \frac{1 + b_i z^{-1}}{1 + a_{i1} z^{-1} + a_{i2} z^{-2}} \protect$ (9.12)

where $ N_d=N/2$ when the number of real poles is even, or $ (N+1)/2$ otherwise. The filter coefficients $ b_i$ and $ a_{ij}$ are now digital second-order section coefficients which can be computed from the continuous-time filter coefficients, if they are known, or they can be directly estimated from discrete-time data.

Expressing complex poles of $ H_d(z)$ in polar form as $ p_i \isdef R_i e^{j\theta_i}$, (where now we assume $ p_i$ denotes a pole in the $ z$ plane), we obtain the classical relations [449]

$\displaystyle a_{i1}$ $\displaystyle =$ $\displaystyle p_i + \overline{p}_i \eqsp 2 R_i \cos(\theta_i) \protect$  
$\displaystyle a_{i2}$ $\displaystyle =$ $\displaystyle \left\vert p_i\right\vert^2 \eqsp R_i^2. \protect$ (9.13)

These parameters are in turn related to the modal parameters resonance frequency $ f_i$ (Hz) and bandwidth $ B_i$ (Hz) by

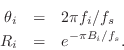
\begin{eqnarray*} \theta_i & = & 2\pi f_i / f_s\\ R_i & = & e^{-\pi B_i/f_s}. \end{eqnarray*}

Often $ f_i$ and $ B_i$ are estimated from a measured log-magnitude frequency-response (see §8.8 for a discussion of various methods).

It remains to determine the overall section gain $ G_i$ in Eq.$ \,$(8.12), and the coefficient $ b_i$ determining the zero location. If $ b_i=0$ (as is common in practice, since the human ear is not very sensitive to spectral nulls), then $ G_i$ can be chosen to match the measured peak height. A particularly simple automatic method is to use least-squares minimization to compute $ G_i$ using Eq.$ \,$(8.12) with $ a_{i1}$ and $ a_{i2}$ fixed (and $ b_i=0$). Generally speaking, least-squares minimization is always immediate when the error to be minimized is linear in the unknown parameter (in this case $ G_i$).

To estimate $ b_i$ in Eq.$ \,$(8.12), an effective method is to work initially with a complex, first-order partial fraction expansion, and use least squares to determine complex gain coefficients $ r_i$ for first-order (complex) terms of the form

$\displaystyle \frac{r_i}{s-p_i} $

as introduced in Eq.$ \,$(8.9) above. The angle and radius of $ p_i$ can still be determined by measuring peaks in the log-magnitude frequency response. When the first-order terms are paired and summed, the $ b_i$ coefficients will ``fall out.''

Sections implementing two real poles are not conveniently specified in terms of resonant frequency and bandwidth. In such cases, it is more common to work with the filter coefficients $ b_i$ and $ a_i$ directly, as they are often computed by system-identification software [288,428] or general purpose filter design utilities, such as in Matlab or Octave [443].

To summarize, numerous techniques exist for estimating modal parameters from measured frequency-response data, and some of these are discussed in §8.8 below. Specifically, resonant modes can be estimated from the magnitude, phase, width, and location of peaks in the Fourier transform of a recorded (or estimated) impulse response Another well known technique is Prony's method [449, p. 393], [297]. There is also a large literature on other methods for estimating the parameters of exponentially decaying sinusoids; examples include the matrix-pencil method [274], and parametric spectrum analysis in general [237].

State Space Approach to Modal Expansions

The preceding discussion of modal synthesis was based primarily on fitting a sum of biquads to measured frequency-response peaks. A more general way of arriving at a modal representation is to first form a state space model of the system [449], and then convert to the modal representation by diagonalizing the state-space model. This approach has the advantage of preserving system behavior between the given inputs and outputs. Specifically, the similarity transform used to diagonalize the system provides new input and output gain vectors which properly excite and observe the system modes precisely as in the original system. This procedure is especially more convenient than the transfer-function based approach above when there are multiple inputs and outputs. For some mathematical details, see [449]9.7For a related worked example, see §C.17.6.

Delay Loop Expansion

When a subset of the resonating modes are nearly harmonically tuned, it can be much more computationally efficient to use a filtered delay loop (see §2.6.5) to generate an entire quasi-harmonic series of modes rather than using a biquad for each modal peak [439]. In this case, the resonator model becomes

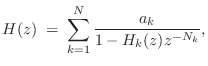
$\displaystyle H(z) \eqsp \sum_{k=1}^N \frac{a_k}{1 - H_k(z) z^{-N_k}}, $

where $ N_k$ is the length of the delay line in the $ k$th comb filter, and $ H_k(z)$ is a low-order filter which can be used to adjust finely the amplitudes and frequencies of the resonances of the $ k$th comb filter [428]. Recall (Chapter 6) that a single filtered delay loop efficiently models a distributed 1D propagation medium such as a vibrating string or acoustic tube. More abstractly, a superposition of such quasi-harmonic mode series can provide a computationally efficient psychoacoustic equivalent approximation to arbitrary collections of modes in the range of human hearing.

Note that when $ H_k(z)$ is close to $ -1$ instead of $ +1$, primarily only odd harmonic resonances are produced, as has been used in modeling the clarinet [431].

Next Section:
Frequency-Response Matching Using Digital Filter Design Methods
Previous Section:
Pole Mapping with Optimal Zeros