Fourier Theorems for the DFT
This chapter derives various Fourier theorems for the case of the DFT. Included are symmetry relations, the shift theorem, convolution theorem, correlation theorem, power theorem, and theorems pertaining to interpolation and downsampling. Applications related to certain theorems are outlined, including linear time-invariant filtering, sampling rate conversion, and statistical signal processing.
The DFT and its Inverse Restated
Let
![]() , denote an
, denote an ![]() -sample complex sequence,
i.e.,
-sample complex sequence,
i.e.,
![]() . Then the spectrum of
. Then the spectrum of ![]() is defined by the
Discrete Fourier Transform (DFT):
is defined by the
Discrete Fourier Transform (DFT):
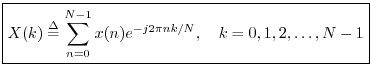

Notation and Terminology
If ![]() is the DFT of
is the DFT of ![]() , we say that
, we say that ![]() and
and ![]() form a transform
pair and write
form a transform
pair and write
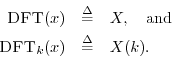
If we need to indicate the length of the DFT explicitly, we will write
![]() and
and
![]() .
As we've already seen, time-domain signals are consistently denoted
using lowercase symbols such as ``
.
As we've already seen, time-domain signals are consistently denoted
using lowercase symbols such as ``![]() ,'' while frequency-domain
signals (spectra), are denoted in uppercase (``
,'' while frequency-domain
signals (spectra), are denoted in uppercase (``
![]() '').
'').
Modulo Indexing, Periodic Extension
The DFT sinusoids
![]() are all periodic
having periods which divide
are all periodic
having periods which divide ![]() . That is,
. That is,
![]() for any
integer
for any
integer ![]() . Since a length
. Since a length ![]() signal
signal ![]() can be expressed as a linear
combination of the DFT sinusoids in the time domain,
can be expressed as a linear
combination of the DFT sinusoids in the time domain,
Moreover, the DFT also repeats naturally every ![]() samples, since
samples, since
Definition (Periodic Extension): For any signal
![]() , we define
, we define
As a result of this convention, all indexing of signals and
spectra7.2 can be interpreted modulo ![]() , and we may write
, and we may write
![]() to emphasize this. Formally, ``
to emphasize this. Formally, ``
![]() '' is defined as
'' is defined as
![]() with
with ![]() chosen to give
chosen to give ![]() in the range
in the range ![]() .
.
As an example, when indexing a spectrum ![]() , we have that
, we have that ![]() which can be interpreted physically as saying that the sampling rate
is the same frequency as dc for discrete time signals. Periodic
extension in the time domain implies that the signal input to the DFT
is mathematically treated as being samples of one period of a
periodic signal, with the period being exactly
which can be interpreted physically as saying that the sampling rate
is the same frequency as dc for discrete time signals. Periodic
extension in the time domain implies that the signal input to the DFT
is mathematically treated as being samples of one period of a
periodic signal, with the period being exactly ![]() seconds (
seconds (![]() samples). The corresponding assumption in the frequency domain is
that the spectrum is exactly zero between frequency samples
samples). The corresponding assumption in the frequency domain is
that the spectrum is exactly zero between frequency samples
![]() . It is also possible to adopt the point of view that the
time-domain signal
. It is also possible to adopt the point of view that the
time-domain signal ![]() consists of
consists of ![]() samples preceded and
followed by zeros. In that case, the spectrum would be
nonzero between spectral samples
samples preceded and
followed by zeros. In that case, the spectrum would be
nonzero between spectral samples ![]() , and the spectrum
between samples would be reconstructed by means of bandlimited
interpolation [72].
, and the spectrum
between samples would be reconstructed by means of bandlimited
interpolation [72].
Signal Operators
It will be convenient in the Fourier theorems of §7.4 to make use of the following signal operator definitions.
Operator Notation
In this book, an operator is defined as a
signal-valued function of a signal. Thus, for the space
of length ![]() complex sequences, an operator
complex sequences, an operator
![]() is a mapping
from
is a mapping
from ![]() to
to ![]() :
:
Note that operator notation is not standard in the field of
digital signal processing. It can be regarded as being influenced by
the field of computer science. In the Fourier theorems below, both
operator and conventional signal-processing notations are provided. In the
author's opinion, operator notation is consistently clearer, allowing
powerful expressions to be written naturally in one line (e.g., see
Eq.![]() (7.8)), and it is much closer to how things look in
a readable computer program (such as in the matlab language).
(7.8)), and it is much closer to how things look in
a readable computer program (such as in the matlab language).
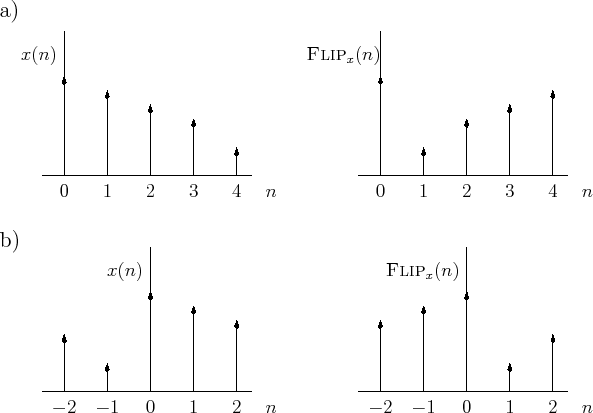
Flip Operator
We define the flip operator by
for all sample indices
Shift Operator
The shift operator is defined by
![\includegraphics[width=\twidth]{eps/shift}](http://www.dsprelated.com/josimages_new/mdft/img1153.png) |
Figure 7.2 illustrates successive one-sample delays of a periodic signal
having first period given by
![]() .
.
Examples
-
![$ \hbox{\sc Shift}_1([1,0,0,0]) = [0,1,0,0]\;$](http://www.dsprelated.com/josimages_new/mdft/img1154.png) (an impulse delayed one sample).
(an impulse delayed one sample).
-
![$ \hbox{\sc Shift}_1([1,2,3,4]) = [4,1,2,3]\;$](http://www.dsprelated.com/josimages_new/mdft/img1155.png) (a circular shift example).
(a circular shift example).
-
![$ \hbox{\sc Shift}_{-2}([1,0,0,0]) = [0,0,1,0]\;$](http://www.dsprelated.com/josimages_new/mdft/img1156.png) (another circular shift example).
(another circular shift example).
Convolution
The convolution of two signals ![]() and
and ![]() in
in ![]() may be
denoted ``
may be
denoted ``
![]() '' and defined by
'' and defined by
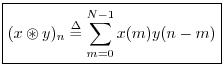
Cyclic convolution can be expressed in terms of previously defined operators as
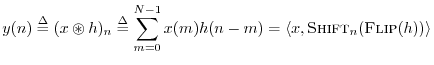
Commutativity of Convolution
Convolution (cyclic or acyclic) is commutative, i.e.,
Proof:
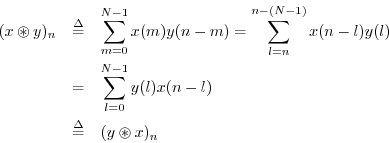
In the first step we made the change of summation variable
![]() , and in the second step, we made use of the fact
that any sum over all
, and in the second step, we made use of the fact
that any sum over all ![]() terms is equivalent to a sum from 0 to
terms is equivalent to a sum from 0 to
![]() .
.
Convolution as a Filtering Operation
In a convolution of two signals
![]() , where both
, where both ![]() and
and ![]() are signals of length
are signals of length ![]() (real or complex), we may interpret either
(real or complex), we may interpret either
![]() or
or ![]() as a filter that operates on the other signal
which is in turn interpreted as the filter's ``input signal''.7.5 Let
as a filter that operates on the other signal
which is in turn interpreted as the filter's ``input signal''.7.5 Let
![]() denote a length
denote a length ![]() signal that is interpreted
as a filter. Then given any input signal
signal that is interpreted
as a filter. Then given any input signal
![]() , the filter output
signal
, the filter output
signal
![]() may be defined as the cyclic convolution of
may be defined as the cyclic convolution of
![]() and
and ![]() :
:
![$\displaystyle \delta(n) = \left\{\begin{array}{ll}
1, & n=0\;\mbox{(mod $N$)} \\ [5pt]
0, & n\ne 0\;\mbox{(mod $N$)}. \\
\end{array} \right.
$](http://www.dsprelated.com/josimages_new/mdft/img1170.png)
![$\displaystyle \delta(n) \isdef \left\{\begin{array}{ll}
1, & n=0 \\ [5pt]
0, & n\ne 0 \\
\end{array} \right.
$](http://www.dsprelated.com/josimages_new/mdft/img1172.png)
As discussed below (§7.2.7), one may embed acyclic convolution within a larger cyclic convolution. In this way, real-world systems may be simulated using fast DFT convolutions (see Appendix A for more on fast convolution algorithms).
Note that only linear, time-invariant (LTI) filters can be completely represented by their impulse response (the filter output in response to an impulse at time 0). The convolution representation of LTI digital filters is fully discussed in Book II [68] of the music signal processing book series (in which this is Book I).
Convolution Example 1: Smoothing a Rectangular Pulse
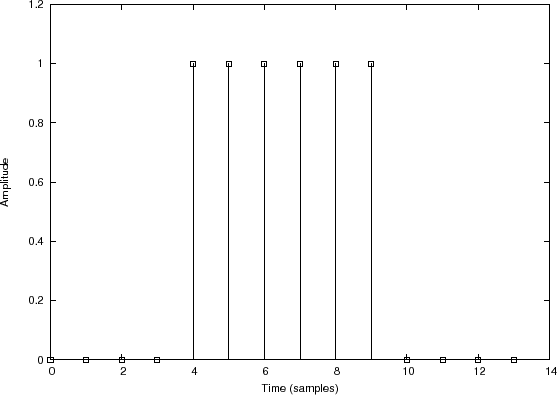
Filter
input signal 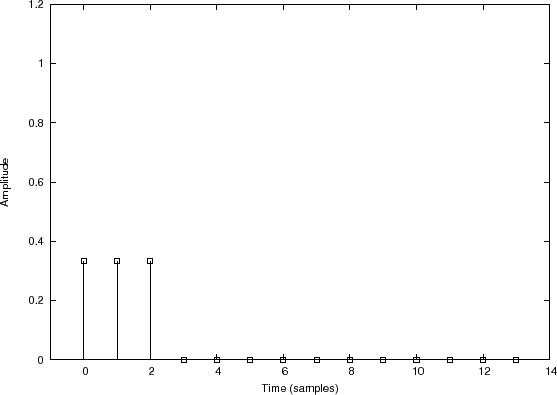
Filter impulse response 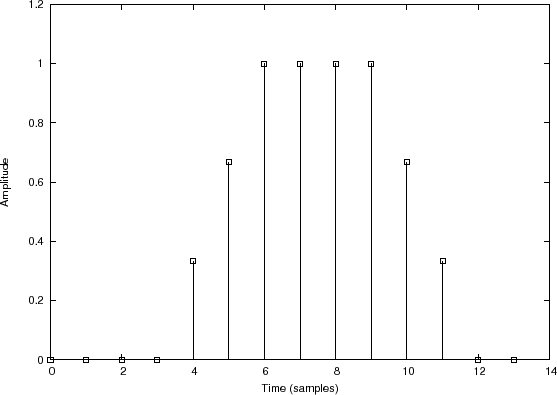
Filter output signal |
Figure 7.3 illustrates convolution of
![$\displaystyle h = \left[\frac{1}{3},\frac{1}{3},\frac{1}{3},0,0,0,0,0,0,0,0,0,0,0\right]
$](http://www.dsprelated.com/josimages_new/mdft/img1177.png)
as graphed in Fig.7.3(c). In this case,
![$\displaystyle h=\left[\frac{1}{3},\frac{1}{3},0,0,0,0,0,0,0,0,0,0,\frac{1}{3}\right]
$](http://www.dsprelated.com/josimages_new/mdft/img1179.png)
Convolution Example 2: ADSR Envelope
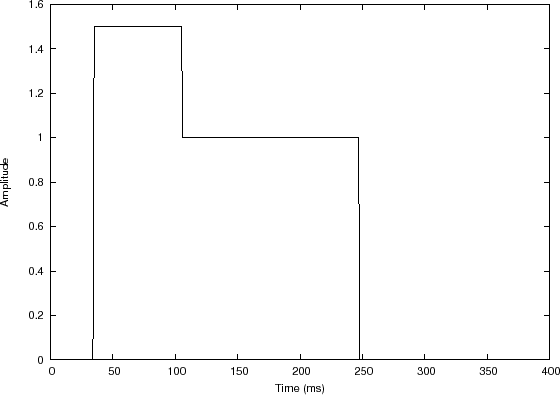
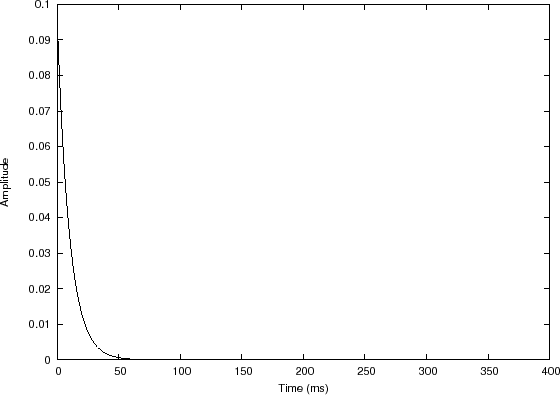
Filter impulse response 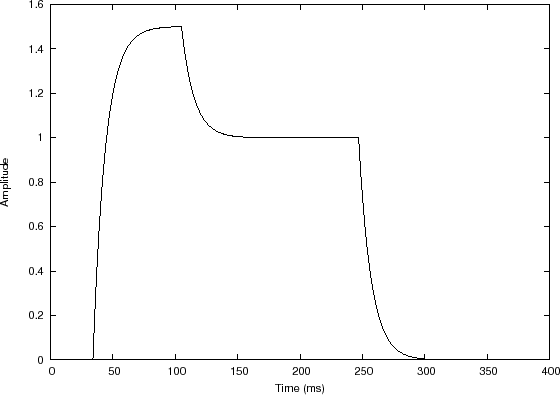
Filter output signal |
In this example, the input signal is a sequence of two rectangular pulses, creating a piecewise constant function, depicted in Fig.7.4(a). The filter impulse response, shown in Fig.7.4(b), is a truncated exponential.7.6
In this example, ![]() is again a causal smoothing-filter impulse
response, and we could call it a ``moving weighted average'', in which
the weighting is exponential into the past. The discontinuous steps
in the input become exponential ``asymptotes'' in the output which are
approached exponentially. The overall appearance of the output signal
resembles what is called an attack, decay, release, and sustain
envelope, or ADSR envelope for short. In a practical ADSR
envelope, the time-constants for attack, decay, and release may be set
independently. In this example, there is only one time constant, that
of
is again a causal smoothing-filter impulse
response, and we could call it a ``moving weighted average'', in which
the weighting is exponential into the past. The discontinuous steps
in the input become exponential ``asymptotes'' in the output which are
approached exponentially. The overall appearance of the output signal
resembles what is called an attack, decay, release, and sustain
envelope, or ADSR envelope for short. In a practical ADSR
envelope, the time-constants for attack, decay, and release may be set
independently. In this example, there is only one time constant, that
of ![]() . The two constant levels in the input signal may be called the
attack level and the sustain level, respectively. Thus,
the envelope approaches the attack level at the attack rate (where the
``rate'' may be defined as the reciprocal of the time constant), it
next approaches the sustain level at the ``decay rate'', and finally,
it approaches zero at the ``release rate''. These envelope parameters
are commonly used in analog synthesizers and their digital
descendants, so-called virtual analog synthesizers. Such an
ADSR envelope is typically used to multiply the output of a waveform
oscillator such as a sawtooth or pulse-train oscillator. For more on
virtual analog synthesis, see, for example,
[78,77].
. The two constant levels in the input signal may be called the
attack level and the sustain level, respectively. Thus,
the envelope approaches the attack level at the attack rate (where the
``rate'' may be defined as the reciprocal of the time constant), it
next approaches the sustain level at the ``decay rate'', and finally,
it approaches zero at the ``release rate''. These envelope parameters
are commonly used in analog synthesizers and their digital
descendants, so-called virtual analog synthesizers. Such an
ADSR envelope is typically used to multiply the output of a waveform
oscillator such as a sawtooth or pulse-train oscillator. For more on
virtual analog synthesis, see, for example,
[78,77].
Convolution Example 3: Matched Filtering
Figure 7.5 illustrates convolution of
![\begin{eqnarray*}
y&=&[1,1,1,1,0,0,0,0] \\
h&=&[1,0,0,0,0,1,1,1]
\end{eqnarray*}](http://www.dsprelated.com/josimages_new/mdft/img1186.png)
to get
For example,
Graphical Convolution
As mentioned above, cyclic convolution can be written as
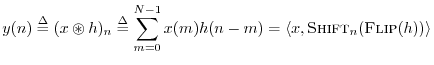
Polynomial Multiplication
Note that when you multiply two polynomials together, their
coefficients are convolved. To see this, let ![]() denote the
denote the
![]() th-order polynomial
th-order polynomial
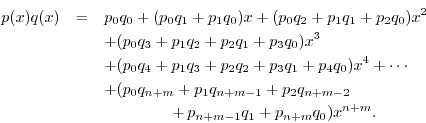
Denoting ![]() by
by
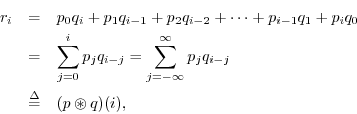
where ![]() and
and ![]() are doubly infinite sequences, defined as
zero for
are doubly infinite sequences, defined as
zero for ![]() and
and ![]() , respectively.
, respectively.
Multiplication of Decimal Numbers
Since decimal numbers are implicitly just polynomials in the powers of 10, e.g.,
Correlation
The correlation operator for two signals ![]() and
and ![]() in
in ![]() is defined as
is defined as
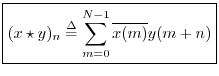
We may interpret the correlation operator as
Stretch Operator
Unlike all previous operators, the
![]() operator maps
a length
operator maps
a length ![]() signal to a length
signal to a length
![]() signal, where
signal, where ![]() and
and ![]() are integers.
We use ``
are integers.
We use ``![]() '' instead of ``
'' instead of ``![]() '' as the time index to underscore this fact.
'' as the time index to underscore this fact.
A stretch by factor ![]() is defined by
is defined by
![$\displaystyle \hbox{\sc Stretch}_{L,m}(x) \isdef
\left\{\begin{array}{ll}
x(...
...x{ an integer} \\ [5pt]
0, & m/L\mbox{ non-integer.} \\
\end{array} \right.
$](http://www.dsprelated.com/josimages_new/mdft/img1217.png)
The stretch operator is used to describe and analyze upsampling,
that is, increasing the sampling rate by an integer factor.
A stretch by ![]() followed by lowpass filtering to the frequency band
followed by lowpass filtering to the frequency band
![]() implements ideal bandlimited interpolation
(introduced in Appendix D).
implements ideal bandlimited interpolation
(introduced in Appendix D).
Zero Padding
Zero padding consists of extending a signal (or spectrum)
with zeros. It maps a length ![]() signal to a length
signal to a length ![]() signal, but
signal, but
![]() need not divide
need not divide ![]() .
.
Definition:
where
Figure 7.7 illustrates zero padding from length ![]() out to length
out to length
![]() . Note that
. Note that ![]() and
and ![]() could be replaced by
could be replaced by ![]() and
and ![]() in the
figure caption.
in the
figure caption.
![\includegraphics[width=\twidth]{eps/zpad}](http://www.dsprelated.com/josimages_new/mdft/img1232.png) |
Note that we have unified the time-domain and frequency-domain
definitions of zero-padding by interpreting the original time axis
![]() as indexing positive-time samples from 0 to
as indexing positive-time samples from 0 to
![]() (for
(for ![]() even), and negative times in the interval
even), and negative times in the interval
![]() .7.8 Furthermore, we require
.7.8 Furthermore, we require
![]() when
when ![]() is even, while odd
is even, while odd ![]() requires no such
restriction. In practice, we often prefer to interpret time-domain
samples as extending from 0 to
requires no such
restriction. In practice, we often prefer to interpret time-domain
samples as extending from 0 to ![]() , i.e., with no negative-time
samples. For this case, we define ``causal zero padding'' as
described below.
, i.e., with no negative-time
samples. For this case, we define ``causal zero padding'' as
described below.
Causal (Periodic) Signals
A signal
![]() may be defined as causal when
may be defined as causal when ![]() for all ``negative-time'' samples (e.g., for
for all ``negative-time'' samples (e.g., for
![]() when
when ![]() is even). Thus, the signal
is even). Thus, the signal
![]() is causal while
is causal while
![]() is not.
For causal signals, zero-padding is equivalent to simply
appending zeros to the original signal. For example,
is not.
For causal signals, zero-padding is equivalent to simply
appending zeros to the original signal. For example,
Causal Zero Padding
In practice, a signal
![]() is often an
is often an ![]() -sample frame of
data taken from some longer signal, and its true starting time can be
anything. In such cases, it is common to treat the start-time of the
frame as zero, with no negative-time samples. In other words,
-sample frame of
data taken from some longer signal, and its true starting time can be
anything. In such cases, it is common to treat the start-time of the
frame as zero, with no negative-time samples. In other words, ![]() represents an
represents an ![]() -sample signal-segment that is translated in time to
start at time 0. In this case (no negative-time samples in the
frame), it is proper to zero-pad by simply appending zeros at the end
of the frame. Thus, we define
e.g.,
-sample signal-segment that is translated in time to
start at time 0. In this case (no negative-time samples in the
frame), it is proper to zero-pad by simply appending zeros at the end
of the frame. Thus, we define
e.g.,
In summary, we have defined two types of zero-padding that arise in practice, which we may term ``causal'' and ``zero-centered'' (or ``zero-phase'', or even ``periodic''). The zero-centered case is the more natural with respect to the mathematics of the DFT, so it is taken as the ``official'' definition of ZEROPAD(). In both cases, however, when properly used, we will have the basic Fourier theorem (§7.4.12 below) stating that zero-padding in the time domain corresponds to ideal bandlimited interpolation in the frequency domain, and vice versa.
Zero Padding Applications
Zero padding in the time domain is used extensively in practice to compute heavily interpolated spectra by taking the DFT of the zero-padded signal. Such spectral interpolation is ideal when the original signal is time limited (nonzero only over some finite duration spanned by the orignal samples).
Note that the time-limited assumption directly contradicts our usual assumption of periodic extension. As mentioned in §6.7, the interpolation of a periodic signal's spectrum from its harmonics is always zero; that is, there is no spectral energy, in principle, between the harmonics of a periodic signal, and a periodic signal cannot be time-limited unless it is the zero signal. On the other hand, the interpolation of a time-limited signal's spectrum is nonzero almost everywhere between the original spectral samples. Thus, zero-padding is often used when analyzing data from a non-periodic signal in blocks, and each block, or frame, is treated as a finite-duration signal which can be zero-padded on either side with any number of zeros. In summary, the use of zero-padding corresponds to the time-limited assumption for the data frame, and more zero-padding yields denser interpolation of the frequency samples around the unit circle.
Sometimes people will say that zero-padding in the time domain yields higher spectral resolution in the frequency domain. However, signal processing practitioners should not say that, because ``resolution'' in signal processing refers to the ability to ``resolve'' closely spaced features in a spectrum analysis (see Book IV [70] for details). The usual way to increase spectral resolution is to take a longer DFT without zero padding--i.e., look at more data. In the field of graphics, the term resolution refers to pixel density, so the common terminology confusion is reasonable. However, remember that in signal processing, zero-padding in one domain corresponds to a higher interpolation-density in the other domain--not a higher resolution.
Ideal Spectral Interpolation
Using Fourier theorems, we will be able to show (§7.4.12) that
zero padding in the time domain gives exact bandlimited interpolation in
the frequency domain.7.9In other words, for truly time-limited signals ![]() ,
taking the DFT of the entire nonzero portion of
,
taking the DFT of the entire nonzero portion of ![]() extended by zeros
yields exact interpolation of the complex spectrum--not an
approximation (ignoring computational round-off error in the DFT
itself). Because the fast Fourier transform (FFT) is so efficient,
zero-padding followed by an FFT is a highly practical method for
interpolating spectra of finite-duration signals, and is used
extensively in practice.
extended by zeros
yields exact interpolation of the complex spectrum--not an
approximation (ignoring computational round-off error in the DFT
itself). Because the fast Fourier transform (FFT) is so efficient,
zero-padding followed by an FFT is a highly practical method for
interpolating spectra of finite-duration signals, and is used
extensively in practice.
Before we can interpolate a spectrum, we must be clear on what a
``spectrum'' really is. As discussed in Chapter 6, the
spectrum of a signal ![]() at frequency
at frequency ![]() is
defined as a complex number
is
defined as a complex number ![]() computed using the inner
product
computed using the inner
product
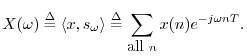
Interpolation Operator
The interpolation operator
![]() interpolates a signal
by an integer factor
interpolates a signal
by an integer factor ![]() using bandlimited interpolation. For
frequency-domain signals
using bandlimited interpolation. For
frequency-domain signals
![]() ,
,
![]() , we may
write spectral interpolation as follows:
, we may
write spectral interpolation as follows:
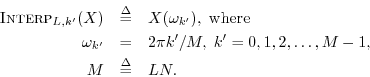
Since
![]() is initially only defined over
the
is initially only defined over
the ![]() roots of unity in the
roots of unity in the ![]() plane, while
plane, while
![]() is defined
over
is defined
over ![]() roots of unity, we define
roots of unity, we define
![]() for
for
![]() by
ideal bandlimited interpolation (specifically time-limited
spectral interpolation in this case).
by
ideal bandlimited interpolation (specifically time-limited
spectral interpolation in this case).
For time-domain signals ![]() , exact interpolation is similarly
bandlimited interpolation, as derived in Appendix D.
, exact interpolation is similarly
bandlimited interpolation, as derived in Appendix D.
Repeat Operator
Like the
![]() and
and
![]() operators, the
operators, the
![]() operator maps a length
operator maps a length ![]() signal to a length
signal to a length
![]() signal:
signal:
Definition: The repeat ![]() times operator is defined for any
times operator is defined for any
![]() by
by
A frequency-domain example is shown in Fig.7.9.
Figure 7.9a shows the original spectrum ![]() , Fig.7.9b
shows the same spectrum plotted over the unit circle in the
, Fig.7.9b
shows the same spectrum plotted over the unit circle in the ![]() plane,
and Fig.7.9c shows
plane,
and Fig.7.9c shows
![]() . The
. The ![]() point (dc) is on
the right-rear face of the enclosing box. Note that when viewed as
centered about
point (dc) is on
the right-rear face of the enclosing box. Note that when viewed as
centered about ![]() ,
, ![]() is a somewhat ``triangularly shaped''
spectrum. We see three copies of this shape in
is a somewhat ``triangularly shaped''
spectrum. We see three copies of this shape in
![]() .
.
![\includegraphics[width=4in]{eps/repeat3d}](http://www.dsprelated.com/josimages_new/mdft/img1263.png) |
The repeat operator is used to state the Fourier theorem
Downsampling Operator
Downsampling by ![]() (also called decimation by
(also called decimation by ![]() ) is defined
for
) is defined
for
![]() as taking every
as taking every ![]() th sample, starting with sample zero:
th sample, starting with sample zero:

The
![]() operator maps a length
operator maps a length ![]() signal down to a length
signal down to a length ![]() signal. It is the inverse of the
signal. It is the inverse of the
![]() operator (but not vice
versa), i.e.,
operator (but not vice
versa), i.e.,
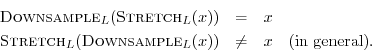
The stretch and downsampling operations do not commute because they are
linear time-varying operators. They can be modeled using
time-varying switches controlled by the sample index ![]() .
.
The following example of
![]() is illustrated in Fig.7.10:
is illustrated in Fig.7.10:
Note that the term ``downsampling'' may also refer to the more
elaborate process of sampling-rate conversion to a lower
sampling rate, in which a signal's sampling rate is lowered by resampling
using bandlimited interpolation. To distinguish these cases, we can call
this bandlimited downsampling, because a lowpass-filter is
needed, in general, prior to downsampling so that aliasing is
avoided. This topic is address in Appendix D. Early
sampling-rate converters were in fact implemented using the
![]() operation, followed by an appropriate lowpass filter,
followed by
operation, followed by an appropriate lowpass filter,
followed by
![]() , in order to implement a sampling-rate
conversion by the factor
, in order to implement a sampling-rate
conversion by the factor ![]() .
.
Alias Operator
Aliasing occurs when a signal is undersampled. If the signal
sampling rate ![]() is too low, we get frequency-domain
aliasing.
is too low, we get frequency-domain
aliasing.
The topic of aliasing normally arises in the context of sampling a continuous-time signal. The sampling theorem (Appendix D) says that we will have no aliasing due to sampling as long as the sampling rate is higher than twice the highest frequency present in the signal being sampled.
In this chapter, we are considering only discrete-time signals, in order to keep the math as simple as possible. Aliasing in this context occurs when a discrete-time signal is downsampled to reduce its sampling rate. You can think of continuous-time sampling as the limiting case for which the starting sampling rate is infinity.
An example of aliasing is shown in Fig.7.11. In the figure, the high-frequency sinusoid is indistinguishable from the lower-frequency sinusoid due to aliasing. We say the higher frequency aliases to the lower frequency.
Undersampling in the frequency domain gives rise to time-domain aliasing. If time or frequency is not specified, the term ``aliasing'' normally means frequency-domain aliasing (due to undersampling in the time domain).
The aliasing operator for ![]() -sample signals
-sample signals
![]() is defined by
is defined by
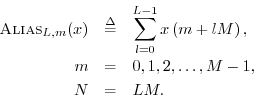
Like the
![]() operator, the
operator, the
![]() operator maps a
length
operator maps a
length ![]() signal down to a length
signal down to a length ![]() signal. A way to think of
it is to partition the original
signal. A way to think of
it is to partition the original ![]() samples into
samples into ![]() blocks of length
blocks of length
![]() , with the first block extending from sample 0 to sample
, with the first block extending from sample 0 to sample ![]() ,
the second block from
,
the second block from ![]() to
to ![]() , etc. Then just add up the blocks.
This process is called aliasing. If the original signal
, etc. Then just add up the blocks.
This process is called aliasing. If the original signal ![]() is
a time signal, it is called time-domain aliasing; if it is a
spectrum, we call it frequency-domain aliasing, or just
aliasing. Note that aliasing is not invertible in general.
Once the blocks are added together, it is usually not possible to
recover the original blocks.
is
a time signal, it is called time-domain aliasing; if it is a
spectrum, we call it frequency-domain aliasing, or just
aliasing. Note that aliasing is not invertible in general.
Once the blocks are added together, it is usually not possible to
recover the original blocks.
Example:
![\begin{eqnarray*}
\hbox{\sc Alias}_2([0,1,2,3,4,5]) &=& [0,1,2] + [3,4,5] = [3,5...
...ox{\sc Alias}_3([0,1,2,3,4,5]) &=& [0,1] + [2,3] + [4,5] = [6,9]
\end{eqnarray*}](http://www.dsprelated.com/josimages_new/mdft/img1280.png)
The alias operator is used to state the Fourier theorem (§7.4.11)
![\includegraphics[width=4.5in]{eps/aliasingfd}](http://www.dsprelated.com/josimages_new/mdft/img1282.png) |
Figure 7.12 shows the result of
![]() applied to
applied to
![]() from Figure 7.9c. Imagine the spectrum of
Fig.7.12a as being plotted on a piece of paper rolled
to form a cylinder, with the edges of the paper meeting at
from Figure 7.9c. Imagine the spectrum of
Fig.7.12a as being plotted on a piece of paper rolled
to form a cylinder, with the edges of the paper meeting at ![]() (upper
right corner of Fig.7.12a). Then the
(upper
right corner of Fig.7.12a). Then the
![]() operation can be
simulated by rerolling the cylinder of paper to cut its circumference in
half. That is, reroll it so that at every point, two sheets of paper
are in contact at all points on the new, narrower cylinder. Now, simply
add the values on the two overlapping sheets together, and you have the
operation can be
simulated by rerolling the cylinder of paper to cut its circumference in
half. That is, reroll it so that at every point, two sheets of paper
are in contact at all points on the new, narrower cylinder. Now, simply
add the values on the two overlapping sheets together, and you have the
![]() of the original spectrum on the unit circle. To alias by
of the original spectrum on the unit circle. To alias by ![]() ,
we would shrink the cylinder further until the paper edges again line up,
giving three layers of paper in the cylinder, and so on.
,
we would shrink the cylinder further until the paper edges again line up,
giving three layers of paper in the cylinder, and so on.
Figure 7.12b shows what is plotted on the first circular wrap of the
cylinder of paper, and Fig.7.12c shows what is on the second wrap.
These are overlaid in Fig.7.12d and added together in
Fig.7.12e. Finally, Figure 7.12f shows both the addition
and the overlay of the two components. We say that the second component
(Fig.7.12c) ``aliases'' to new frequency components, while the
first component (Fig.7.12b) is considered to be at its original
frequencies. If the unit circle of Fig.7.12a covers frequencies
0 to ![]() , all other unit circles (Fig.7.12b-c) cover
frequencies 0 to
, all other unit circles (Fig.7.12b-c) cover
frequencies 0 to ![]() .
.
In general, aliasing by the factor ![]() corresponds to a
sampling-rate reduction by the factor
corresponds to a
sampling-rate reduction by the factor ![]() . To prevent aliasing
when reducing the sampling rate, an anti-aliasing lowpass
filter is generally used. The lowpass filter attenuates all signal
components at frequencies outside the interval
. To prevent aliasing
when reducing the sampling rate, an anti-aliasing lowpass
filter is generally used. The lowpass filter attenuates all signal
components at frequencies outside the interval
![]() so that all frequency components which would alias are first removed.
so that all frequency components which would alias are first removed.
Conceptually, in the frequency domain, the unit circle is reduced by
![]() to a unit circle
half the original size, where the two halves are summed. The inverse
of aliasing is then ``repeating'' which should be understood as
increasing the unit circle circumference using ``periodic
extension'' to generate ``more spectrum'' for the larger unit circle.
In the time domain, on the other hand, downsampling is the inverse of
the stretch operator. We may interchange ``time'' and ``frequency''
and repeat these remarks. All of these relationships are precise only
for integer stretch/downsampling/aliasing/repeat factors; in
continuous time and frequency, the restriction to integer factors is
removed, and we obtain the (simpler) scaling theorem (proved
in §C.2).
to a unit circle
half the original size, where the two halves are summed. The inverse
of aliasing is then ``repeating'' which should be understood as
increasing the unit circle circumference using ``periodic
extension'' to generate ``more spectrum'' for the larger unit circle.
In the time domain, on the other hand, downsampling is the inverse of
the stretch operator. We may interchange ``time'' and ``frequency''
and repeat these remarks. All of these relationships are precise only
for integer stretch/downsampling/aliasing/repeat factors; in
continuous time and frequency, the restriction to integer factors is
removed, and we obtain the (simpler) scaling theorem (proved
in §C.2).
Even and Odd Functions
Some of the Fourier theorems can be succinctly expressed in terms of even and odd symmetries.
Definition: A function ![]() is said to be even if
is said to be even if
![]() .
.
An even function is also symmetric, but the term symmetric applies also to functions symmetric about a point other than 0.
Definition: A function ![]() is said to be odd if
is said to be odd if
![]() .
.
An odd function is also called antisymmetric.
Note that every finite odd function ![]() must satisfy
must satisfy
![]() .7.11 Moreover, for any
.7.11 Moreover, for any
![]() with
with
![]() even, we also have
even, we also have ![]() since
since
![]() ; that is,
; that is, ![]() and
and ![]() index
the same point when
index
the same point when ![]() is even.
is even.
Theorem: Every function ![]() can be decomposed into a sum of its even part
can be decomposed into a sum of its even part
![]() and odd part
and odd part ![]() , where
, where
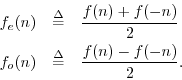
Proof: In the above definitions, ![]() is even and
is even and ![]() is odd by construction.
Summing, we have
is odd by construction.
Summing, we have
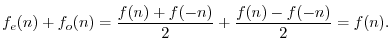
Theorem: The product of even functions is even, the product of odd functions
is even, and the product of an even times an odd function is odd.
Proof: Readily shown.
Since even times even is even, odd times odd is even, and even times odd is
odd, we can think of even as ![]() and odd as
and odd as ![]() :
:
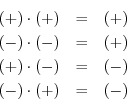
Example:
![]() ,
,
![]() , is an
even signal since
, is an
even signal since
![]() .
.
Example:
![]() is an odd signal since
is an odd signal since
![]() .
.
Example:
![]() is an odd signal (even times odd).
is an odd signal (even times odd).
Example:
![]() is an even signal (odd times odd).
is an even signal (odd times odd).
Theorem: The sum of all the samples of an odd signal ![]() in
in ![]() is zero.
is zero.
Proof: This is readily shown by writing the sum as
![]() , where the last term only occurs when
, where the last term only occurs when ![]() is even. Each
term so written is zero for an odd signal
is even. Each
term so written is zero for an odd signal ![]() .
.
Example: For all DFT sinusoidal frequencies
![]() ,
,
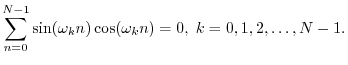
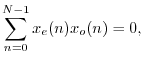
Fourier Theorems
In this section the main Fourier theorems are stated and proved. It is no small matter how simple these theorems are in the DFT case relative to the other three cases (DTFT, Fourier transform, and Fourier series, as defined in Appendix B). When infinite summations or integrals are involved, the conditions for the existence of the Fourier transform can be quite difficult to characterize mathematically. Mathematicians have expended a considerable effort on such questions. By focusing primarily on the DFT case, we are able to study the essential concepts conveyed by the Fourier theorems without getting involved with mathematical difficulties.
Linearity
Theorem: For any
![]() and
and
![]() , the DFT satisfies
, the DFT satisfies
Proof:
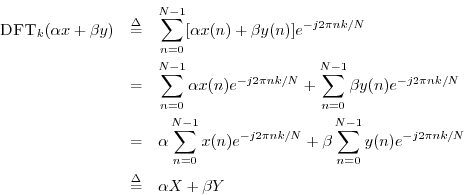
Conjugation and Reversal
Theorem: For any
![]() ,
,
Proof:

Theorem: For any
![]() ,
,
Proof: Making the change of summation variable
![]() , we get
, we get
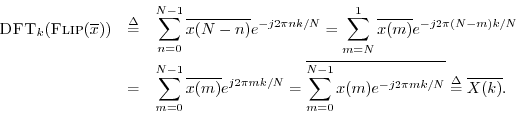
Theorem: For any
![]() ,
,
Proof:
![\begin{eqnarray*}
\hbox{\sc DFT}_k[\hbox{\sc Flip}(x)] &\isdef & \sum_{n=0}^{N-1...
...-1}x(m) e^{j 2\pi mk/N} \isdef X(-k) \isdef \hbox{\sc Flip}_k(X)
\end{eqnarray*}](http://www.dsprelated.com/josimages_new/mdft/img1326.png)
Corollary:
For any
![]() ,
,
Proof: Picking up the previous proof at the third formula, remembering that ![]() is real,
is real,
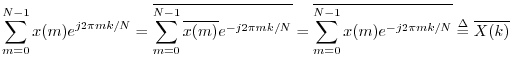
Thus, conjugation in the frequency domain corresponds to reversal in the time domain. Another way to say it is that negating spectral phase flips the signal around backwards in time.
Corollary:
For any
![]() ,
,
Proof: This follows from the previous two cases.
Definition: The property
![]() is called Hermitian symmetry
or ``conjugate symmetry.'' If
is called Hermitian symmetry
or ``conjugate symmetry.'' If
![]() , it may be called
skew-Hermitian.
, it may be called
skew-Hermitian.
Another way to state the preceding corollary is
Symmetry
In the previous section, we found
![]() when
when ![]() is
real. This fact is of high practical importance. It says that the
spectrum of every real signal is Hermitian.
Due to this symmetry, we may discard all negative-frequency spectral
samples of a real signal and regenerate them later if needed from the
positive-frequency samples. Also, spectral plots of real signals are
normally displayed only for positive frequencies; e.g., spectra of
sampled signals are normally plotted over the range 0 Hz to
is
real. This fact is of high practical importance. It says that the
spectrum of every real signal is Hermitian.
Due to this symmetry, we may discard all negative-frequency spectral
samples of a real signal and regenerate them later if needed from the
positive-frequency samples. Also, spectral plots of real signals are
normally displayed only for positive frequencies; e.g., spectra of
sampled signals are normally plotted over the range 0 Hz to ![]() Hz. On the other hand, the spectrum of a complex signal must
be shown, in general, from
Hz. On the other hand, the spectrum of a complex signal must
be shown, in general, from ![]() to
to ![]() (or from 0 to
(or from 0 to ![]() ),
since the positive and negative frequency components of a complex
signal are independent.
),
since the positive and negative frequency components of a complex
signal are independent.
Recall from §7.3 that a signal ![]() is said to be
even if
is said to be
even if
![]() , and odd if
, and odd if
![]() . Below
are are Fourier theorems pertaining to even and odd signals and/or
spectra.
. Below
are are Fourier theorems pertaining to even and odd signals and/or
spectra.
Theorem: If
![]() , then
re
, then
re![]() is even and
im
is even and
im![]() is odd.
is odd.
Proof: This follows immediately from the conjugate symmetry of ![]() for real signals
for real signals
![]() .
.
Theorem: If
![]() ,
,
![]() is even and
is even and ![]() is odd.
is odd.
Proof: This follows immediately from the conjugate symmetry of ![]() expressed
in polar form
expressed
in polar form
![]() .
.
The conjugate symmetry of spectra of real signals is perhaps the most important symmetry theorem. However, there are a couple more we can readily show:
Theorem: An even signal has an even transform:
Proof:
Express ![]() in terms of its real and imaginary parts by
in terms of its real and imaginary parts by
![]() . Note that for a complex signal
. Note that for a complex signal ![]() to be even, both its real and
imaginary parts must be even. Then
to be even, both its real and
imaginary parts must be even. Then
Let even
![\begin{eqnarray*}
X(k)&=&\sum_{n=0}^{N-1}\mbox{even}_n\cdot\mbox{even}_{nk}
+ ...
...10pt]
&=& \mbox{even}_k + j \cdot \mbox{even}_k = \mbox{even}_k.
\end{eqnarray*}](http://www.dsprelated.com/josimages_new/mdft/img1356.png)
Theorem: A real even signal has a real even transform:
Proof: This follows immediately from setting ![]() in the preceding
proof. From Eq.
in the preceding
proof. From Eq.![]() (7.5), we are left with
(7.5), we are left with
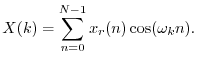
Instead of adapting the previous proof, we can show it directly:
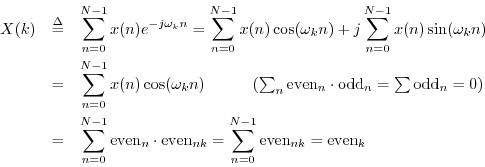
Definition: A signal with a real spectrum (such as any real, even signal)
is often called a zero phase signal. However, note that when
the spectrum goes negative (which it can), the phase is really
![]() , not 0. When a real spectrum is positive at dc (i.e.,
, not 0. When a real spectrum is positive at dc (i.e.,
![]() ), it is then truly zero-phase over at least some band
containing dc (up to the first zero-crossing in frequency). When the
phase switches between 0 and
), it is then truly zero-phase over at least some band
containing dc (up to the first zero-crossing in frequency). When the
phase switches between 0 and ![]() at the zero-crossings of the
(real) spectrum, the spectrum oscillates between being zero phase and
``constant phase''. We can say that all real spectra are
piecewise constant-phase spectra, where the two constant values
are 0 and
at the zero-crossings of the
(real) spectrum, the spectrum oscillates between being zero phase and
``constant phase''. We can say that all real spectra are
piecewise constant-phase spectra, where the two constant values
are 0 and ![]() (or
(or ![]() , which is the same phase as
, which is the same phase as ![]() ). In
practice, such zero-crossings typically occur at low magnitude, such
as in the ``side-lobes'' of the DTFT of a ``zero-centered symmetric
window'' used for spectrum analysis (see Chapter 8 and Book IV
[70]).
). In
practice, such zero-crossings typically occur at low magnitude, such
as in the ``side-lobes'' of the DTFT of a ``zero-centered symmetric
window'' used for spectrum analysis (see Chapter 8 and Book IV
[70]).
Shift Theorem
Theorem: For any
![]() and any integer
and any integer ![]() ,
,
Proof:
![\begin{eqnarray*}
\hbox{\sc DFT}_k[\hbox{\sc Shift}_\Delta(x)] &\isdef & \sum_{n...
...}x(m) e^{-j 2\pi mk/N} \\
&\isdef & e^{-j \omega_k \Delta} X(k)
\end{eqnarray*}](http://www.dsprelated.com/josimages_new/mdft/img1365.png)
The shift theorem is often expressed in shorthand as
Linear Phase Terms
The reason
![]() is called a linear phase term is
that its phase is a linear function of frequency:
is called a linear phase term is
that its phase is a linear function of frequency:
Linear Phase Signals
In practice, a signal may be said to be linear phase when its phase is of the form
Zero Phase Signals
A zero-phase signal is thus a linear-phase signal for which the
phase-slope ![]() is zero. As mentioned above (in
§7.4.3), it would be more precise to say ``0-or-
is zero. As mentioned above (in
§7.4.3), it would be more precise to say ``0-or-![]() -phase
signal'' instead of ``zero-phase signal''. Another better term is
``zero-centered signal'', since every real (even) spectrum corresponds
to an even (real) signal. Of course, a zero-centered symmetric signal
is simply an even signal, by definition. Thus, a ``zero-phase
signal'' is more precisely termed an ``even signal''.
-phase
signal'' instead of ``zero-phase signal''. Another better term is
``zero-centered signal'', since every real (even) spectrum corresponds
to an even (real) signal. Of course, a zero-centered symmetric signal
is simply an even signal, by definition. Thus, a ``zero-phase
signal'' is more precisely termed an ``even signal''.
Application of the Shift Theorem to FFT Windows
In practical spectrum analysis, we most often use the Fast
Fourier Transform7.15 (FFT) together with a
window function
![]() . As discussed
further in Chapter 8, windows are normally positive (
. As discussed
further in Chapter 8, windows are normally positive (![]() ),
symmetric about their midpoint, and look pretty much like a ``bell
curve.'' A window multiplies the signal
),
symmetric about their midpoint, and look pretty much like a ``bell
curve.'' A window multiplies the signal ![]() being analyzed to form a
windowed signal
being analyzed to form a
windowed signal
![]() , or
, or
![]() , which
is then analyzed using an FFT. The window serves to taper the
data segment gracefully to zero, thus eliminating spectral distortions
due to suddenly cutting off the signal in time. Windowing is thus
appropriate when
, which
is then analyzed using an FFT. The window serves to taper the
data segment gracefully to zero, thus eliminating spectral distortions
due to suddenly cutting off the signal in time. Windowing is thus
appropriate when ![]() is a short section of a longer signal (not a
period or whole number of periods from a periodic signal).
is a short section of a longer signal (not a
period or whole number of periods from a periodic signal).
Theorem: Real symmetric FFT windows are linear phase.
Proof: Let ![]() denote the window samples for
denote the window samples for
![]() .
Since the window is symmetric, we have
.
Since the window is symmetric, we have
![]() for all
for all ![]() .
When
.
When ![]() is odd, there is a sample at the midpoint at time
is odd, there is a sample at the midpoint at time
![]() . The midpoint can be translated to the time origin to
create an even signal. As established on page
. The midpoint can be translated to the time origin to
create an even signal. As established on page ![]() ,
the DFT of a real and even signal is real and even. By the shift
theorem, the DFT of the original symmetric window is a real, even
spectrum multiplied by a linear phase term, yielding a spectrum
having a phase that is linear in frequency with possible
discontinuities of
,
the DFT of a real and even signal is real and even. By the shift
theorem, the DFT of the original symmetric window is a real, even
spectrum multiplied by a linear phase term, yielding a spectrum
having a phase that is linear in frequency with possible
discontinuities of ![]() radians. Thus, all odd-length real
symmetric signals are ``linear phase'', including FFT windows.
radians. Thus, all odd-length real
symmetric signals are ``linear phase'', including FFT windows.
When ![]() is even, the window midpoint at time
is even, the window midpoint at time ![]() lands
half-way between samples, so we cannot simply translate the window to
zero-centered form. However, we can still factor the window spectrum
lands
half-way between samples, so we cannot simply translate the window to
zero-centered form. However, we can still factor the window spectrum
![]() into the product of a linear phase term
into the product of a linear phase term
![]() and a real spectrum (verify this as an
exercise), which satisfies the definition of a linear phase signal.
and a real spectrum (verify this as an
exercise), which satisfies the definition of a linear phase signal.
Convolution Theorem
Theorem: For any
![]() ,
,
Proof:
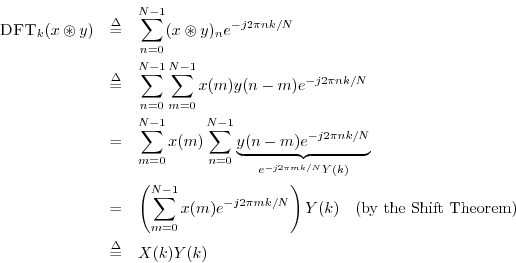
This is perhaps the most important single Fourier theorem of all. It
is the basis of a large number of FFT applications. Since an FFT
provides a fast Fourier transform, it also provides fast
convolution, thanks to the convolution theorem. It turns out that
using an FFT to perform convolution is really more efficient in
practice only for reasonably long convolutions, such as ![]() . For
much longer convolutions, the savings become enormous compared with
``direct'' convolution. This happens because direct convolution
requires on the order of
. For
much longer convolutions, the savings become enormous compared with
``direct'' convolution. This happens because direct convolution
requires on the order of ![]() operations (multiplications and
additions), while FFT-based convolution requires on the order of
operations (multiplications and
additions), while FFT-based convolution requires on the order of
![]() operations, where
operations, where ![]() denotes the logarithm-base-2 of
denotes the logarithm-base-2 of
![]() (see §A.1.2 for an explanation).
(see §A.1.2 for an explanation).
The simple matlab example in Fig.7.13 illustrates how much faster
convolution can be performed using an FFT.7.16 We see that
for a length ![]() convolution, the fft function is
approximately 300 times faster in Octave, and 30 times faster in
Matlab. (The conv routine is much faster in Matlab, even
though it is a built-in function in both cases.)
convolution, the fft function is
approximately 300 times faster in Octave, and 30 times faster in
Matlab. (The conv routine is much faster in Matlab, even
though it is a built-in function in both cases.)
N = 1024; % FFT much faster at this length t = 0:N-1; % [0,1,2,...,N-1] h = exp(-t); % filter impulse reponse H = fft(h); % filter frequency response x = ones(1,N); % input = dc (any signal will do) Nrep = 100; % number of trials to average t0 = clock; % latch the current time for i=1:Nrep, y = conv(x,h); end % Direct convolution t1 = etime(clock,t0)*1000; % elapsed time in msec t0 = clock; for i=1:Nrep, y = ifft(fft(x) .* H); end % FFT convolution t2 = etime(clock,t0)*1000; disp(sprintf([... 'Average direct-convolution time = %0.2f msec\n',... 'Average FFT-convolution time = %0.2f msec\n',... 'Ratio = %0.2f (Direct/FFT)'],... t1/Nrep,t2/Nrep,t1/t2)); % =================== EXAMPLE RESULTS =================== Octave: Average direct-convolution time = 69.49 msec Average FFT-convolution time = 0.23 msec Ratio = 296.40 (Direct/FFT) Matlab: Average direct-convolution time = 15.73 msec Average FFT-convolution time = 0.50 msec Ratio = 31.46 (Direct/FFT) |
A similar program produced the results for different FFT lengths shown
in Table 7.1.7.17 In this software environment, the fft function
is faster starting with length ![]() , and it is never significantly
slower at short lengths, where ``calling overhead'' dominates.
, and it is never significantly
slower at short lengths, where ``calling overhead'' dominates.
|
A table similar to Table 7.1 in Strum and Kirk
[79, p. 521], based on the number of real
multiplies, finds that the fft is faster starting at length ![]() ,
and that direct convolution is significantly faster for very short
convolutions (e.g., 16 operations for a direct length-4 convolution,
versus 176 for the fft function).
,
and that direct convolution is significantly faster for very short
convolutions (e.g., 16 operations for a direct length-4 convolution,
versus 176 for the fft function).
See Appendix A for further discussion of FFT algorithms and their applications.
Dual of the Convolution Theorem
The dual7.18 of the convolution theorem says that multiplication in the time domain is convolution in the frequency domain:
Theorem:

Proof: The steps are the same as in the convolution theorem.
This theorem also bears on the use of FFT windows. It implies
that
windowing in the time domain corresponds to
smoothing in the frequency domain.
That is, the spectrum of
![]() is simply
is simply ![]() filtered by
filtered by ![]() , or,
, or,
![]() . This
smoothing reduces sidelobes associated with the
rectangular window, which is the window one is using implicitly
when a data frame
. This
smoothing reduces sidelobes associated with the
rectangular window, which is the window one is using implicitly
when a data frame ![]() is considered time limited and therefore
eligible for ``windowing'' (and zero-padding). See Chapter 8 and
Book IV [70] for further discussion.
is considered time limited and therefore
eligible for ``windowing'' (and zero-padding). See Chapter 8 and
Book IV [70] for further discussion.
Correlation Theorem
Theorem: For all
![]() ,
,
Proof:
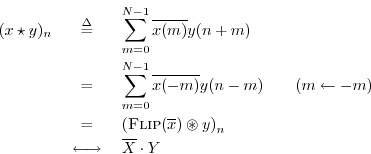
The last step follows from the convolution theorem and the result
![]() from §7.4.2. Also, the
summation range in the second line is equivalent to the range
from §7.4.2. Also, the
summation range in the second line is equivalent to the range
![]() because all indexing is modulo
because all indexing is modulo ![]() .
.
Power Theorem
Theorem: For all
![]() ,
,
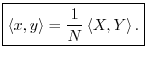
Proof:
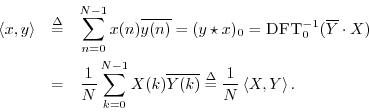
As mentioned in §5.8, physical power is
energy per unit time.7.19 For example, when a force produces a motion,
the power delivered is given by the force times the
velocity of the motion. Therefore, if ![]() and
and ![]() are in
physical units of force and velocity (or any analogous quantities such
as voltage and current, etc.), then their product
are in
physical units of force and velocity (or any analogous quantities such
as voltage and current, etc.), then their product
![]() is proportional to the power per sample at time
is proportional to the power per sample at time ![]() ,
and
,
and
![]() becomes proportional to the total energy
supplied (or absorbed) by the driving force. By the power theorem,
becomes proportional to the total energy
supplied (or absorbed) by the driving force. By the power theorem,
![]() can be interpreted as the energy per bin in
the DFT, or spectral power, i.e., the energy associated with a
spectral band of width
can be interpreted as the energy per bin in
the DFT, or spectral power, i.e., the energy associated with a
spectral band of width ![]() .7.20
.7.20
Normalized DFT Power Theorem
Note that the power theorem would be more elegant if the DFT were defined as the coefficient of projection onto the normalized DFT sinusoids
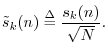
Rayleigh Energy Theorem (Parseval's Theorem)
Theorem:
For any
![]() ,
,
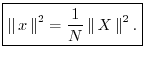
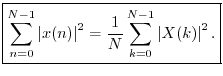
Proof: This is a special case of the power theorem.
Note that again the relationship would be cleaner (
![]() )
if we were using the normalized DFT.
)
if we were using the normalized DFT.
Stretch Theorem (Repeat Theorem)
Theorem: For all
![]() ,
,
Proof:
Recall the stretch operator:
![$\displaystyle \hbox{\sc Stretch}_{L,m}(x) \isdef
\left\{\begin{array}{ll}
x(...
...=\mbox{integer} \\ [5pt]
0, & m/L\neq \mbox{integer} \\
\end{array} \right.
$](http://www.dsprelated.com/josimages_new/mdft/img1430.png)

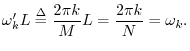
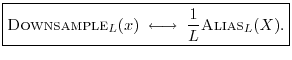
Downsampling Theorem (Aliasing Theorem)
Theorem: For all
![]() ,
,
Proof: Let
![]() denote the frequency index in the
aliased spectrum, and
let
denote the frequency index in the
aliased spectrum, and
let
![]() . Then
. Then ![]() is length
is length ![]() ,
where
,
where ![]() is the downsampling factor. We have
is the downsampling factor. We have
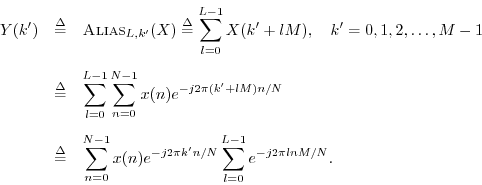
Since ![]() , the sum over
, the sum over ![]() becomes
becomes
![$\displaystyle \sum_{l=0}^{L-1}\left[e^{-j2\pi n/L}\right]^l =
\frac{1-e^{-j2\p...
...ht) \\ [5pt]
0, & n\neq 0 \left(\mbox{mod}\;L\right) \\
\end{array} \right.
$](http://www.dsprelated.com/josimages_new/mdft/img1447.png)
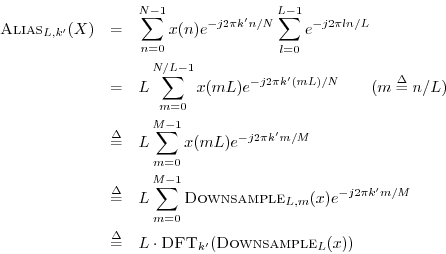
Since the above derivation also works in reverse, the theorem is proved.
An illustration of aliasing in the frequency domain is shown in Fig.7.12.
Illustration of the Downsampling/Aliasing Theorem in Matlab
>> N=4; >> x = 1:N; >> X = fft(x); >> x2 = x(1:2:N); >> fft(x2) % FFT(Downsample(x,2)) ans = 4 -2 >> (X(1:N/2) + X(N/2 + 1:N))/2 % (1/2) Alias(X,2) ans = 4 -2
Zero Padding Theorem (Spectral Interpolation)
A fundamental tool in practical spectrum analysis is zero padding. This theorem shows that zero padding in the time domain corresponds to ideal interpolation in the frequency domain (for time-limited signals):
Theorem: For any
![]()
Proof: Let ![]() with
with ![]() . Then
. Then
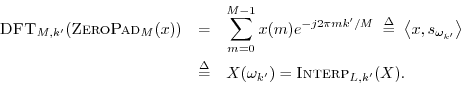
Thus, this theorem follows directly from the definition of the ideal
interpolation operator
![]() . See §8.1.3 for an
example of zero-padding in spectrum analysis.
. See §8.1.3 for an
example of zero-padding in spectrum analysis.
Periodic Interpolation (Spectral Zero Padding)
The dual of the zero-padding theorem states formally that zero padding in the frequency domain corresponds to periodic interpolation in the time domain:
Definition: For all
![]() and any integer
and any integer ![]() ,
,
where zero padding is defined in §7.2.7 and illustrated in Figure 7.7. In other words, zero-padding a DFT by the factor
Periodic interpolation is ideal for signals that are periodic
in ![]() samples, where
samples, where ![]() is the DFT length. For non-periodic
signals, which is almost always the case in practice, bandlimited
interpolation should be used instead (Appendix D).
is the DFT length. For non-periodic
signals, which is almost always the case in practice, bandlimited
interpolation should be used instead (Appendix D).
Relation to Stretch Theorem
It is instructive to interpret the periodic interpolation theorem in
terms of the stretch theorem,
![]() .
To do this, it is convenient to define a ``zero-centered rectangular
window'' operator:
.
To do this, it is convenient to define a ``zero-centered rectangular
window'' operator:
Definition: For any
![]() and any odd integer
and any odd integer ![]() we define the
length
we define the
length ![]() even rectangular windowing operation by
even rectangular windowing operation by
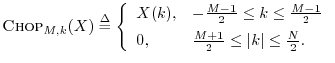
Theorem: When
![]() consists of one or more periods from a periodic
signal
consists of one or more periods from a periodic
signal
![]() ,
,
Proof: First, recall that
![]() . That is,
stretching a signal by the factor
. That is,
stretching a signal by the factor ![]() gives a new signal
gives a new signal
![]() which has a spectrum
which has a spectrum ![]() consisting of
consisting of ![]() copies of
copies of
![]() repeated around the unit circle. The ``baseband copy'' of
repeated around the unit circle. The ``baseband copy'' of ![]() in
in
![]() can be defined as the
can be defined as the ![]() -sample sequence centered about frequency
zero. Therefore, we can use an ``ideal filter'' to ``pass'' the
baseband spectral copy and zero out all others, thereby converting
-sample sequence centered about frequency
zero. Therefore, we can use an ``ideal filter'' to ``pass'' the
baseband spectral copy and zero out all others, thereby converting
![]() to
to
![]() . I.e.,
. I.e.,
Bandlimited Interpolation of Time-Limited Signals
The previous result can be extended toward bandlimited interpolation
of
![]() which includes all nonzero samples from an
arbitrary time-limited signal
which includes all nonzero samples from an
arbitrary time-limited signal
![]() (i.e., going beyond the interpolation of only periodic bandlimited
signals given one or more periods
(i.e., going beyond the interpolation of only periodic bandlimited
signals given one or more periods
![]() ) by
) by
- replacing the rectangular window
 with a
smoother spectral window
with a
smoother spectral window  , and
, and
- using extra zero-padding in the time domain to convert the
cyclic convolution between
 and
and  into an
acyclic convolution between them (recall §7.2.4).
into an
acyclic convolution between them (recall §7.2.4).
The approximation symbol `
Equation (7.8) can provide the basis for a high-quality
sampling-rate conversion algorithm. Arbitrarily long signals can be
accommodated by breaking them into segments of length ![]() , applying
the above algorithm to each block, and summing the up-sampled blocks using
overlap-add. That is, the lowpass filter
, applying
the above algorithm to each block, and summing the up-sampled blocks using
overlap-add. That is, the lowpass filter ![]() ``rings''
into the next block and possibly beyond (or even into both adjacent
time blocks when
``rings''
into the next block and possibly beyond (or even into both adjacent
time blocks when ![]() is not causal), and this ringing must be summed
into all affected adjacent blocks. Finally, the filter
is not causal), and this ringing must be summed
into all affected adjacent blocks. Finally, the filter ![]() can
``window away'' more than the top
can
``window away'' more than the top ![]() copies of
copies of ![]() in
in ![]() , thereby
preparing the time-domain signal for downsampling, say by
, thereby
preparing the time-domain signal for downsampling, say by
![]() :
:
DFT Theorems Problems
See http://ccrma.stanford.edu/~jos/mdftp/DFT_Theorems_Problems.html
Next Section:
Example Applications of the DFT
Previous Section:
Derivation of the Discrete Fourier Transform (DFT)








![$\displaystyle y = x\circledast h = \left[0,0,0,0,\frac{1}{3},\frac{2}{3},1,1,1,1,\frac{2}{3},\frac{1}{3},0,0\right] \protect$](http://www.dsprelated.com/josimages_new/mdft/img1178.png)
![\includegraphics[width=2.5in]{eps/conv}](http://www.dsprelated.com/josimages_new/mdft/img1185.png)
![\includegraphics[width=4in]{eps/stretch}](http://www.dsprelated.com/josimages_new/mdft/img1216.png)
![$\displaystyle \hbox{\sc ZeroPad}_{M,m}(x) \isdef \left\{\begin{array}{ll} x(m),...
...ert m\vert < N/2 \\ [5pt] 0, & \mbox{otherwise} \\ \end{array} \right. \protect$](http://www.dsprelated.com/josimages_new/mdft/img1223.png)
![\includegraphics[width=\twidth]{eps/repeat}](http://www.dsprelated.com/josimages_new/mdft/img1261.png)
![\includegraphics[width=4in]{eps/downsamplex}](http://www.dsprelated.com/josimages_new/mdft/img1271.png)
![\includegraphics[scale=0.5]{eps/aliasing}](http://www.dsprelated.com/josimages_new/mdft/img1275.png)
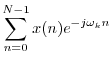
![$\displaystyle \sum_{n=0}^{N-1}[x_r(n)+jx_i(n)] \cos(\omega_k n) - j [x_r(n)+jx_i(n)] \sin(\omega_k n)$](http://www.dsprelated.com/josimages_new/mdft/img1348.png)
![$\displaystyle \sum_{n=0}^{N-1}[x_r(n)\cos(\omega_k n) + x_i(n)\sin(\omega_k n)]$](http://www.dsprelated.com/josimages_new/mdft/img1349.png)












