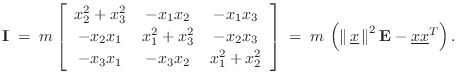Rigid-Body Dynamics
Below are selected topics from rigid-body dynamics, a subtopic of classical mechanics involving the use of Newton's laws of motion to solve for the motion of rigid bodies moving in 1D, 2D, or 3D space.B.11 We may think of a rigid body as a distributed mass, that is, a mass that has length, area, and/or volume rather than occupying only a single point in space. Rigid body models have application in stiff strings (modeling them as disks of mass interconnect by ideal springs), rigid bridges, resonator braces, and so on.
We have already used Newton's ![]() to formulate mathematical dynamic
models for the ideal point-mass (§B.1.1), spring
(§B.1.3), and a simple mass-spring system (§B.1.4).
Since many physical systems can be modeled as assemblies of masses and
(normally damped) springs, we are pretty far along already. However,
when the springs interconnecting our point-masses are very stiff, we
may approximate them as rigid to simplify our simulations. Thus,
rigid bodies can be considered mass-spring systems in which the
springs are so stiff that they can be treated as rigid massless rods
(infinite spring-constants
to formulate mathematical dynamic
models for the ideal point-mass (§B.1.1), spring
(§B.1.3), and a simple mass-spring system (§B.1.4).
Since many physical systems can be modeled as assemblies of masses and
(normally damped) springs, we are pretty far along already. However,
when the springs interconnecting our point-masses are very stiff, we
may approximate them as rigid to simplify our simulations. Thus,
rigid bodies can be considered mass-spring systems in which the
springs are so stiff that they can be treated as rigid massless rods
(infinite spring-constants ![]() , in the notation of §B.1.3).
, in the notation of §B.1.3).
So, what is new about distributed masses, as opposed to the point-masses considered previously? As we will see, the main new ingredient is rotational dynamics. The total momentum of a rigid body (distributed mass) moving through space will be described as the sum of the linear momentum of its center of mass (§B.4.1 below) plus the angular momentum about its center of mass (§B.4.13 below).
Center of Mass
The center of mass (or centroid) of a rigid body is
found by averaging the spatial points of the body
![]() weighted by the mass
weighted by the mass ![]() of those points:B.12
of those points:B.12
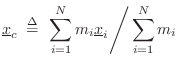
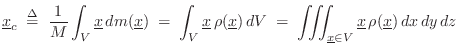
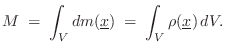
A nice property of the center of mass is that gravity acts on a far-away object as if all its mass were concentrated at its center of mass. For this reason, the center of mass is often called the center of gravity.
Linear Momentum of the Center of Mass
Consider a system of ![]() point-masses
point-masses ![]() , each traveling with
vector velocity
, each traveling with
vector velocity
![]() , and not necessarily rigidly attached to
each other. Then the total momentum of the system is
, and not necessarily rigidly attached to
each other. Then the total momentum of the system is
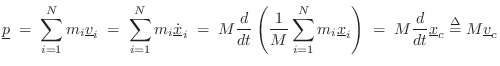
Thus, the momentum
![]() of any collection of masses
of any collection of masses ![]() (including rigid bodies) equals the total mass
(including rigid bodies) equals the total mass ![]() times the
velocity of the center-of-mass.
times the
velocity of the center-of-mass.
Whoops, No Angular Momentum!
The previous result might be surprising since we said at the outset that we were going to decompose the total momentum into a sum of linear plus angular momentum. Instead, we found that the total momentum is simply that of the center of mass, which means any angular momentum that might have been present just went away. (The center of mass is just a point that cannot rotate in a measurable way.) Angular momentum does not contribute to linear momentum, so it provides three new ``degrees of freedom'' (three new energy storage dimensions, in 3D space) that are ``missed'' when considering only linear momentum.
To obtain the desired decomposition of momentum into linear plus angular momentum, we will choose a fixed reference point in space (usually the center of mass) and then, with respect to that reference point, decompose an arbitrary mass-particle travel direction into the sum of two mutually orthogonal vector components: one will be the vector component pointing radially with respect to the fixed point (for the ``linear momentum'' component), and the other will be the vector component pointing tangentially with respect to the fixed point (for the ``angular momentum''), as shown in Fig.B.3. When the reference point is the center of mass, the resultant radial force component gives us the force on the center of mass, which creates linear momentum, while the net tangential component (times distance from the center-of-mass) give us a resultant torque about the reference point, which creates angular momentum. As we saw above, because the tangential force component does not contribute to linear momentum, we can simply sum the external force vectors and get the same result as summing their radial components. These topics will be discussed further below, after some elementary preliminaries.
![\includegraphics[width=1.5in]{eps/rigidbody}](http://www.dsprelated.com/josimages_new/pasp/img2710.png) |
Translational Kinetic Energy
The translational kinetic energy of a collection of masses
![]() is given by
is given by
More generally, the total energy of a collection of masses (including distributed and/or rigidly interconnected point-masses) can be expressed as the sum of the translational and rotational kinetic energies [270, p. 98].
Rotational Kinetic Energy
![\includegraphics[width=1.2in]{eps/masscircle}](http://www.dsprelated.com/josimages_new/pasp/img2715.png) |
The rotational kinetic energy of a rigid assembly of masses (or
mass distribution) is the sum of the rotational kinetic energies of
the component masses. Therefore, consider a point-mass ![]() rotatingB.13 in a circular orbit
of radius
rotatingB.13 in a circular orbit
of radius ![]() and angular velocity
and angular velocity ![]() (radians per second), as
shown in Fig.B.4. To make it a closed system, we can
imagine an effectively infinite mass at the origin
(radians per second), as
shown in Fig.B.4. To make it a closed system, we can
imagine an effectively infinite mass at the origin
![]() . Then the
speed of the mass along the circle is
. Then the
speed of the mass along the circle is ![]() , and its kinetic
energy is
, and its kinetic
energy is
![]() . Since this is what we want
for the rotational kinetic energy of the system, it is
convenient to define it in terms of angular velocity
. Since this is what we want
for the rotational kinetic energy of the system, it is
convenient to define it in terms of angular velocity ![]() in
radians per second. Thus, we write
in
radians per second. Thus, we write
where
is called the mass moment of inertia.
Mass Moment of Inertia
The mass moment of inertia ![]() (or simply moment of
inertia), plays the role of mass in rotational dynamics, as
we saw in
Eq.
(or simply moment of
inertia), plays the role of mass in rotational dynamics, as
we saw in
Eq.![]() (B.7) above.
(B.7) above.
The mass moment of inertia of a rigid body, relative to a given axis of rotation, is given by a weighted sum over its mass, with each mass-point weighted by the square of its distance from the rotation axis. Compare this with the center of mass (§B.4.1) in which each mass-point is weighted by its vector location in space (and divided by the total mass).
Equation (B.8) above gives the moment of inertia for a single point-mass
![]() rotating a distance
rotating a distance ![]() from the axis to be
from the axis to be ![]() . Therefore,
for a rigid collection of point-masses
. Therefore,
for a rigid collection of point-masses ![]() ,
,
![]() ,B.14 the
moment of inertia about a given axis of rotation is obtained by adding
the component moments of inertia:
,B.14 the
moment of inertia about a given axis of rotation is obtained by adding
the component moments of inertia:
where
For a continuous mass distribution, the moment of inertia is given by integrating the contribution of each differential mass element:
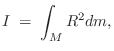 |
(B.10) |
where
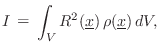
Circular Disk Rotating in Its Own Plane
For example, the moment of inertia for a uniform circular disk of
total mass ![]() and radius
and radius ![]() , rotating in its own plane about a
rotation axis piercing its center, is given by
, rotating in its own plane about a
rotation axis piercing its center, is given by
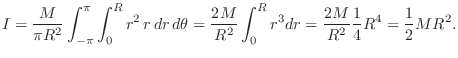
Circular Disk Rotating About Its Diameter
The moment of inertia for the same circular disk rotating about an axis in the plane of the disk, passing through its center, is given by
![$\displaystyle I = \frac{M}{\pi R^2}\cdot 4\int_0^{\pi/2} \int_0^R [r\cos(\theta)]^2\, r\,dr\,d\theta
= \frac{1}{4}MR^2
$](http://www.dsprelated.com/josimages_new/pasp/img2728.png)
Perpendicular Axis Theorem
In general, for any 2D distribution of mass, the moment of inertia
about an axis orthogonal to the plane of the mass equals the sum of
the moments of inertia about any two mutually orthogonal axes in the
plane of the mass intersecting the first axis. To see this, consider
an arbitrary mass element ![]() having rectilinear coordinates
having rectilinear coordinates
![]() in the plane of the mass. (All three coordinate axes
intersect at a point in the mass-distribution plane.) Then its moment
of inertia about the axis orthogonal to the mass plane is
in the plane of the mass. (All three coordinate axes
intersect at a point in the mass-distribution plane.) Then its moment
of inertia about the axis orthogonal to the mass plane is
![]() while its moment of inertia about coordinate axes
within the mass-plane are respectively
while its moment of inertia about coordinate axes
within the mass-plane are respectively ![]() and
and ![]() .
This, the perpendicular axis theorem is an immediate consequence of
the Pythagorean theorem for right triangles.
.
This, the perpendicular axis theorem is an immediate consequence of
the Pythagorean theorem for right triangles.
Parallel Axis Theorem
Let ![]() denote the moment of inertia for a rotation axis passing
through the center of mass, and let
denote the moment of inertia for a rotation axis passing
through the center of mass, and let ![]() denote
the moment of inertia for a rotation axis parallel to the first
but a distance
denote
the moment of inertia for a rotation axis parallel to the first
but a distance ![]() away from it. Then the parallel axis theorem
says that
away from it. Then the parallel axis theorem
says that
Stretch Rule
Note that the moment of inertia does not change when masses are moved
along a vector parallel to the axis of rotation (see, e.g.,
Eq.![]() (B.9)). Thus, any rigid body may be ``stretched'' or
``squeezed'' parallel to the rotation axis without changing its moment
of inertia. This is known as the stretch rule, and it can be
used to simplify geometry when finding the moment of inertia.
(B.9)). Thus, any rigid body may be ``stretched'' or
``squeezed'' parallel to the rotation axis without changing its moment
of inertia. This is known as the stretch rule, and it can be
used to simplify geometry when finding the moment of inertia.
For example, we saw in §B.4.4 that the moment of inertia
of a point-mass ![]() a distance
a distance ![]() from the axis of rotation is given
by
from the axis of rotation is given
by ![]() . By the stretch rule, the same applies to an ideal
rod of mass
. By the stretch rule, the same applies to an ideal
rod of mass ![]() parallel to and distance
parallel to and distance ![]() from the axis of
rotation.
from the axis of
rotation.
Note that mass can be also be ``stretched'' along the circle of
rotation without changing the moment of inertia for the mass about
that axis. Thus, the point mass ![]() can be stretched out to form a
mass ring at radius
can be stretched out to form a
mass ring at radius ![]() about the axis of rotation without
changing its moment of inertia about that axis. Similarly, the ideal
rod of the previous paragraph can be stretched tangentially to form a
cylinder of radius
about the axis of rotation without
changing its moment of inertia about that axis. Similarly, the ideal
rod of the previous paragraph can be stretched tangentially to form a
cylinder of radius ![]() and mass
and mass ![]() , with its axis of symmetry
coincident with the axis of rotation. In all of these examples, the
moment of inertia is
, with its axis of symmetry
coincident with the axis of rotation. In all of these examples, the
moment of inertia is ![]() about the axis of rotation.
about the axis of rotation.
Area Moment of Inertia
The area moment of inertia is the second moment of an area ![]() around a given axis:
around a given axis:
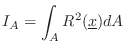
Comparing with the definition of mass moment of inertia in §B.4.4 above, we see that mass is replaced by area in the area moment of inertia.
In a planar mass distribution with total mass ![]() uniformly
distributed over an area
uniformly
distributed over an area ![]() (i.e., a constant mass density of
(i.e., a constant mass density of
![]() ), the mass moment of inertia
), the mass moment of inertia ![]() is given by the area
moment of inertia
is given by the area
moment of inertia ![]() times mass-density
times mass-density ![]() :
:
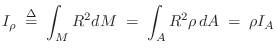
Radius of Gyration
For a planar distribution of mass rotating about some axis in the plane of the mass, the radius of gyration is the distance from the axis that all mass can be concentrated to obtain the same mass moment of inertia. Thus, the radius of gyration is the ``equivalent distance'' of the mass from the axis of rotation. In this context, gyration can be defined as rotation of a planar region about some axis lying in the plane.
For a bar cross-section with area ![]() , the radius of gyration is given by
, the radius of gyration is given by
where
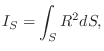
Rectangular Cross-Section
For a rectangular cross-section of height ![]() and width
and width ![]() , area
, area
![]() , the area moment of inertia about the horizontal midline is
given by
, the area moment of inertia about the horizontal midline is
given by
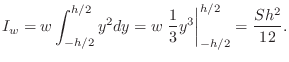
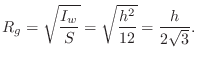
The radius of gyration can be thought of as the ``effective radius'' of the mass distribution with respect to its inertial response to rotation (``gyration'') about the chosen axis.
Most cross-sectional shapes (e.g., rectangular), have at least two radii of gyration. A circular cross-section has only one, and its radius of gyration is equal to half its radius, as shown in the next section.
Circular Cross-Section
For a circular cross-section of radius ![]() , Eq.
, Eq.![]() (B.11) tells us
that the squared radius of gyration about any line passing through the
center of the cross-section is given by
(B.11) tells us
that the squared radius of gyration about any line passing through the
center of the cross-section is given by
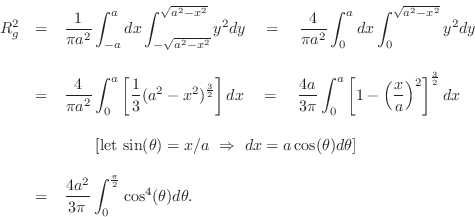
Using the elementrary trig identity
![]() , we readily
derive
, we readily
derive
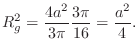
For a circular tube in which the mass of the cross-section lies
within a circular annulus having inner radius ![]() and outer
radius
and outer
radius ![]() , the radius of gyration is given by
, the radius of gyration is given by
Two Masses Connected by a Rod
As an introduction to the decomposition of rigid-body motion into
translational and rotational components, consider the
simple system shown in Fig.B.5. The excitation force
densityB.15 ![]() can be
applied anywhere between
can be
applied anywhere between ![]() and
and ![]() along the connecting rod.
We will deliver a vertical impulse of momentum to the mass on the
right, and show, among other observations, that the total kinetic
energy is split equally into (1) the rotational kinetic energy
about the center of mass, and (2) the translational kinetic
energy of the total mass, treated as being located at the center of
mass. This is accomplished by defining a new frame of
reference (i.e., a moving coordinate system) that has its origin at
the center of mass.
along the connecting rod.
We will deliver a vertical impulse of momentum to the mass on the
right, and show, among other observations, that the total kinetic
energy is split equally into (1) the rotational kinetic energy
about the center of mass, and (2) the translational kinetic
energy of the total mass, treated as being located at the center of
mass. This is accomplished by defining a new frame of
reference (i.e., a moving coordinate system) that has its origin at
the center of mass.
First, note that the driving-point impedance (§7.1)
``seen'' by the driving force ![]() varies as a function of
varies as a function of ![]() .
At
.
At ![]() , The excitation
, The excitation ![]() sees a ``point mass''
sees a ``point mass'' ![]() , and no
rotation is excited by the force (by symmetry). At
, and no
rotation is excited by the force (by symmetry). At ![]() , on the
other hand, the excitation
, on the
other hand, the excitation
![]() only sees mass
only sees mass ![]() at time
0, because the vertical motion of either point-mass initially only
rotates the other point-mass via the massless connecting rod. Thus,
an observation we can make right away is that the driving point
impedance seen by
at time
0, because the vertical motion of either point-mass initially only
rotates the other point-mass via the massless connecting rod. Thus,
an observation we can make right away is that the driving point
impedance seen by ![]() depends on the striking point
depends on the striking point ![]() and,
away from
and,
away from ![]() , it depends on time
, it depends on time ![]() as well.
as well.
To avoid dealing with a time-varying driving-point impedance, we will
use an impulsive force input at time ![]() . Since momentum is the
time-integral of force (
. Since momentum is the
time-integral of force (
![]() ), our
excitation will be a unit momentum transferred to the two-mass
system at time 0.
), our
excitation will be a unit momentum transferred to the two-mass
system at time 0.
Striking the Rod in the Middle
First, consider
![]() . That is, we apply an
upward unit-force impulse at time 0 in the middle of the rod. The
total momentum delivered in the neighborhood of
. That is, we apply an
upward unit-force impulse at time 0 in the middle of the rod. The
total momentum delivered in the neighborhood of ![]() and
and ![]() is
obtained by integrating the applied force density with respect to time
and position:
is
obtained by integrating the applied force density with respect to time
and position:
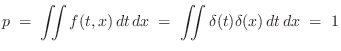
The kinetic energy of the system after time zero is
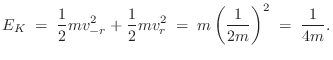
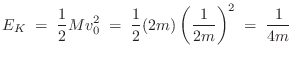
Striking One of the Masses
Now let
![]() . That is, we apply an impulse
of vertical momentum to the mass on the right at time 0.
. That is, we apply an impulse
of vertical momentum to the mass on the right at time 0.
In this case, the unit of vertical momentum is transferred entirely to the mass on the right, so that
Note that the velocity of the center-of-mass ![]() is the
same as it was when we hit the midpoint of the rod. This is an
important general equivalence: The sum of all external force vectors
acting on a rigid body can be applied as a single resultant force
vector to the total mass concentrated at the center of mass to find
the linear (translational) motion produced. (Recall from §B.4.1
that such a sum is the same as the sum of all radially acting external
force components, since the tangential components contribute only to
rotation and not to translation.)
is the
same as it was when we hit the midpoint of the rod. This is an
important general equivalence: The sum of all external force vectors
acting on a rigid body can be applied as a single resultant force
vector to the total mass concentrated at the center of mass to find
the linear (translational) motion produced. (Recall from §B.4.1
that such a sum is the same as the sum of all radially acting external
force components, since the tangential components contribute only to
rotation and not to translation.)
All of the kinetic energy is in the mass on the right just after time zero:
However, after time zero, things get more complicated, because the mass on the left gets dragged into a rotation about the center of mass.
To simplify ongoing analysis, we can define a body-fixed frame
of referenceB.16 having its origin at the center of mass. Let ![]() denote a velocity in this frame. Since the velocity of the center of
mass is
denote a velocity in this frame. Since the velocity of the center of
mass is
![]() , we can convert any velocity
, we can convert any velocity ![]() in the
body-fixed frame to a velocity
in the
body-fixed frame to a velocity ![]() in the original frame by adding
in the original frame by adding
![]() to it, viz.,
to it, viz.,
In the body-fixed frame, all kinetic energy is rotational about
the origin. Recall (Eq.![]() (B.9)) that the moment of inertia for this
system, with respect to the center of mass at
(B.9)) that the moment of inertia for this
system, with respect to the center of mass at ![]() , is
, is
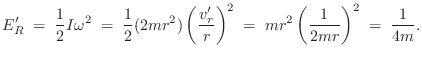
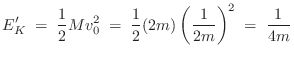
In summary, we defined a moving body-fixed frame having its origin at the center-of-mass, and the total kinetic energy was computed to be
It is important to note that, after time zero, both the linear
momentum of the center-of-mass (
![]() ), and the angular momentum in the body-fixed frame
(
), and the angular momentum in the body-fixed frame
(
![]() ) remain
constant over time.B.17 In the original space-fixed
frame, on the other hand, there is a complex transfer of momentum back
and forth between the masses after time zero.
) remain
constant over time.B.17 In the original space-fixed
frame, on the other hand, there is a complex transfer of momentum back
and forth between the masses after time zero.
Similarly, the translational kinetic energy of the total mass, treated as being concentrated at its center-of-mass, and the rotational kinetic energy in the body-fixed frame, are both constant after time zero, while in the space-fixed frame, kinetic energy transfers back and forth between the two masses. At all times, however, the total kinetic energy is the same in both formulations.
Angular Velocity Vector
When working with rotations, it is convenient to define the
angular-velocity vector as a vector
![]() pointing
along the axis of rotation. There are two directions we could
choose from, so we pick the one corresponding to the right-hand
rule, i.e., when the fingers of the right hand curl in the direction
of the rotation, the thumb points in the direction of the angular
velocity vector.B.18 The
length
pointing
along the axis of rotation. There are two directions we could
choose from, so we pick the one corresponding to the right-hand
rule, i.e., when the fingers of the right hand curl in the direction
of the rotation, the thumb points in the direction of the angular
velocity vector.B.18 The
length
![]() should obviously equal the angular
velocity
should obviously equal the angular
velocity ![]() . It is convenient also to work with a unit-length
variant
. It is convenient also to work with a unit-length
variant
![]() .
.
As introduced in Eq.![]() (B.8) above, the mass moment of inertia is
given by
(B.8) above, the mass moment of inertia is
given by ![]() where
where ![]() is the distance from the (instantaneous)
axis of rotation to the mass
is the distance from the (instantaneous)
axis of rotation to the mass ![]() located at
located at
![]() . In
terms of the angular-velocity vector
. In
terms of the angular-velocity vector
![]() , we can write this as
(see Fig.B.6)
, we can write this as
(see Fig.B.6)
where

![\includegraphics[width=1.5in]{eps/pxov}](http://www.dsprelated.com/josimages_new/pasp/img2806.png) |
Using the vector cross product (defined in the next section),
we will show (in §B.4.17) that ![]() can be written more succinctly as
can be written more succinctly as
Vector Cross Product
The vector cross product (or simply vector product, as
opposed to the scalar product (which is also called the
dot product, or inner product)) is commonly used in
vector calculus--a basic mathematical toolset used in
mechanics [270,258],
acoustics [349], electromagnetism [356], quantum
mechanics, and more. It can be defined symbolically in the form of
a matrix determinant:B.19
where
The second and third lines of Eq.![]() (B.15) make it clear that
(B.15) make it clear that
![]() . This is one example of a host of identities that
one learns in vector calculus and its applications.
. This is one example of a host of identities that
one learns in vector calculus and its applications.
Cross-Product Magnitude
It is a straightforward exercise to show that the cross-product magnitude is equal to the product of the vector lengths times the sine of the angle between them:B.21
where
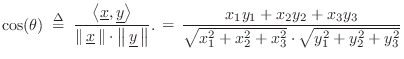
To derive Eq.![]() (B.16), let's begin with the cross-product in matrix
form as
(B.16), let's begin with the cross-product in matrix
form as
![]() using the first matrix form in the
third line of the cross-product definition in Eq.
using the first matrix form in the
third line of the cross-product definition in Eq.![]() (B.15) above. Then
(B.15) above. Then
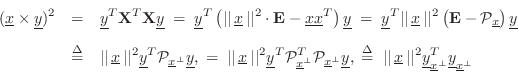
where
![]() denotes the identity matrix in
denotes the identity matrix in
![]() ,
,
![]() denotes the orthogonal-projection matrix onto
denotes the orthogonal-projection matrix onto
![]() [451],
[451],
![]() denotes the projection matrix onto
the orthogonal complement of
denotes the projection matrix onto
the orthogonal complement of
![]() ,
,
![]() denotes the component of
denotes the component of
![]() orthogonal to
orthogonal to
![]() , and we used the fact that orthogonal projection matrices
, and we used the fact that orthogonal projection matrices
![]() are idempotent (i.e.,
are idempotent (i.e.,
![]() ) and
symmetric (when real, as we have here) when we replaced
) and
symmetric (when real, as we have here) when we replaced
![]() by
by
![]() above. Finally,
note that the length of
above. Finally,
note that the length of
![]() is
is
![]() , where
, where ![]() is the angle
between the 1D subspaces spanned by
is the angle
between the 1D subspaces spanned by
![]() and
and
![]() in the plane
including both vectors. Thus,
in the plane
including both vectors. Thus,
The direction of the cross-product vector is then taken to be
orthogonal to both
![]() and
and
![]() according to the right-hand
rule. This orthogonality can be checked by verifying that
according to the right-hand
rule. This orthogonality can be checked by verifying that
![]() . The right-hand-rule parity can be checked by
rotating the space so that
. The right-hand-rule parity can be checked by
rotating the space so that
![]() and
and
![]() in
which case
in
which case
![]() . Thus, the cross
product points ``up'' relative to the
. Thus, the cross
product points ``up'' relative to the
![]() plane for
plane for
![]() and ``down'' for
and ``down'' for
![]() .
.
Mass Moment of Inertia as a Cross Product
In Eq.![]() (B.14) above, the mass moment of inertia was expressed
in terms of orthogonal projection as
(B.14) above, the mass moment of inertia was expressed
in terms of orthogonal projection as
![]() , where
, where
![]() . In terms of the vector cross
product, we can now express it as
. In terms of the vector cross
product, we can now express it as
Tangential Velocity as a Cross Product
Referring again to Fig.B.4, we can write the
tangential velocity vector
![]() as a vector cross product of
the angular-velocity vector
as a vector cross product of
the angular-velocity vector
![]() (§B.4.11) and the position
vector
(§B.4.11) and the position
vector
![]() :
:
To see this, let's first check its direction and then its magnitude. By the right-hand rule,
Angular Momentum
The angular momentum of a mass ![]() rotating in a circle of
radius
rotating in a circle of
radius ![]() with angular velocity
with angular velocity ![]() (rad/s), is defined by
(rad/s), is defined by
Relation of Angular to Linear Momentum
Recall (§B.3) that the momentum of a mass ![]() traveling
with velocity
traveling
with velocity ![]() in a straight line is given by
in a straight line is given by
Thus, the angular momentum
Linear momentum can be viewed as a renormalized special case of angular momentum in which the radius of rotation goes to infinity.
Angular Momentum Vector
Like linear momentum, angular momentum is fundamentally a vector in
![]() . The definition of the previous section suffices when the
direction does not change, in which case we can focus only on its
magnitude
. The definition of the previous section suffices when the
direction does not change, in which case we can focus only on its
magnitude ![]() .
.
More generally, let
![]() denote the 3-space coordinates
of a point-mass
denote the 3-space coordinates
of a point-mass ![]() , and let
, and let
![]() denote its velocity
in
denote its velocity
in ![]() . Then the instantaneous angular momentum vector
of the mass relative to the origin (not necessarily rotating about a
fixed axis) is given by
. Then the instantaneous angular momentum vector
of the mass relative to the origin (not necessarily rotating about a
fixed axis) is given by
where
For the special case in which
![]() is orthogonal to
is orthogonal to
![]() , as in Fig.B.4, we have that
, as in Fig.B.4, we have that
![]() points, by the right-hand rule, in the direction of the angular
velocity vector
points, by the right-hand rule, in the direction of the angular
velocity vector
![]() (up out of the page), which is
satisfying. Furthermore, its magnitude is given by
(up out of the page), which is
satisfying. Furthermore, its magnitude is given by
In the more general case of an arbitrary mass velocity vector
![]() , we know from §B.4.12 that the magnitude of
, we know from §B.4.12 that the magnitude of
![]() equals the product of the distance from the axis
of rotation to the mass, i.e.,
equals the product of the distance from the axis
of rotation to the mass, i.e.,
![]() , times the length of
the component of
, times the length of
the component of
![]() that is orthogonal to
that is orthogonal to
![]() , i.e.,
, i.e.,
![]() , as needed.
, as needed.
It can be shown that vector angular momentum, as defined, is conserved.B.22 For example, in an orbit, such as that of the moon around the earth, or that of Halley's comet around the sun, the orbiting object speeds up as it comes closer to the object it is orbiting. (See Kepler's laws of planetary motion.) Similarly, a spinning ice-skater spins faster when pulling in arms to reduce the moment of inertia about the spin axis. The conservation of angular momentum can be shown to result from the principle of least action and the isotrophy of space [270, p. 18].
Angular Momentum Vector in Matrix Form
The two cross-products in Eq.![]() (B.19) can be written out with the help
of the vector analysis identityB.23
(B.19) can be written out with the help
of the vector analysis identityB.23
where
![$\displaystyle \mathbf{I}\underline{\omega}\eqsp
\left[\begin{array}{ccc}
I_{1...
...begin{array}{c} \omega_1 \\ [2pt] \omega_2 \\ [2pt] \omega_3\end{array}\right]
$](http://www.dsprelated.com/josimages_new/pasp/img2872.png)
The matrix
The vector angular momentum of a rigid body is obtained by summing the angular momentum of its constituent mass particles. Thus,
In summary, the angular momentum vector
![]() is given by the mass
moment of inertia tensor
is given by the mass
moment of inertia tensor
![]() times the angular-velocity vector
times the angular-velocity vector
![]() representing the axis of rotation.
representing the axis of rotation.
Note that the angular momentum vector
![]() does not in general
point in the same direction as the angular-velocity vector
does not in general
point in the same direction as the angular-velocity vector
![]() . We
saw above that it does in the special case of a point mass traveling
orthogonal to its position vector. In general,
. We
saw above that it does in the special case of a point mass traveling
orthogonal to its position vector. In general,
![]() and
and
![]() point
in the same direction whenever
point
in the same direction whenever
![]() is an eigenvector of
is an eigenvector of
![]() , as will be discussed further below (§B.4.16). In this
case, the rigid body is said to be dynamically balanced.B.24
, as will be discussed further below (§B.4.16). In this
case, the rigid body is said to be dynamically balanced.B.24
Mass Moment of Inertia Tensor
As derived in the previous section, the moment of inertia
tensor, in 3D Cartesian coordinates, is a three-by-three matrix
![]() that can be multiplied by any angular-velocity vector to
produce the corresponding angular momentum vector for either a point
mass or a rigid mass distribution. Note that the origin of the
angular-velocity vector
that can be multiplied by any angular-velocity vector to
produce the corresponding angular momentum vector for either a point
mass or a rigid mass distribution. Note that the origin of the
angular-velocity vector
![]() is always fixed at
is always fixed at
![]() in the space
(typically located at the center of mass). Therefore, the moment of
inertia tensor
in the space
(typically located at the center of mass). Therefore, the moment of
inertia tensor
![]() is defined relative to that origin.
is defined relative to that origin.
The moment of inertia tensor can similarly be used to compute the
mass moment of inertia for any normalized angular velocity
vector
![]() as
as
Since rotational energy is defined as
We can show Eq.
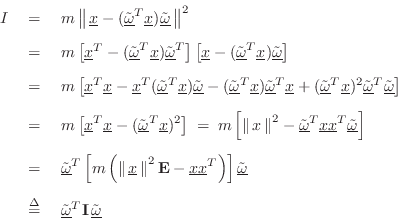
where again
![]() denotes the three-by-three identity matrix, and
denotes the three-by-three identity matrix, and
which agrees with Eq.
For a collection of ![]() masses
masses ![]() located at
located at
![]() , we
simply sum over their masses to add up the moments of inertia:
, we
simply sum over their masses to add up the moments of inertia:
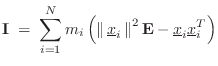
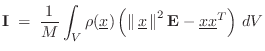
Simple Example
Consider a mass ![]() at
at
![]() . Then the mass moment of inertia
tensor is
. Then the mass moment of inertia
tensor is
![$\displaystyle \mathbf{I}\eqsp m \left(\left\Vert\,\underline{x}\,\right\Vert^2\...
...ay}{ccc}
0 & 0 & 0\\ [2pt]
0 & 1 & 0\\ [2pt]
0 & 0 & 1
\end{array}\right].
$](http://www.dsprelated.com/josimages_new/pasp/img2891.png)
![\begin{displaymath}
I \eqsp \underline{\tilde{\omega}}^T\mathbf{I}\,\underline{\...
...{array}{c} 1 \\ [2pt] 0 \\ [2pt] 0\end{array}\right]m \eqsp 0.
\end{displaymath}](http://www.dsprelated.com/josimages_new/pasp/img2893.png)
![$\displaystyle I \eqsp \underline{\tilde{\omega}}^T\mathbf{I}\,\underline{\tilde...
...]
\left[\begin{array}{c} 0 \\ [2pt] 1 \\ [2pt] 0\end{array}\right] \eqsp m x^2
$](http://www.dsprelated.com/josimages_new/pasp/img2895.png)
Example with Coupled Rotations
Now let the mass ![]() be located at
be located at
![]() so that
so that
![\begin{eqnarray*}
\mathbf{I}&=& m \left(\left\Vert\,\underline{x}\,\right\Vert^2...
... & 0\\ [2pt]
-1 & 1 & 0\\ [2pt]
0 & 0 & 2
\end{array}\right].
\end{eqnarray*}](http://www.dsprelated.com/josimages_new/pasp/img2897.png)
We expect
![]() to yield zero for the moment of inertia, and
sure enough
to yield zero for the moment of inertia, and
sure enough
![]() . Similarly, the vector angular
momentum is zero, since
. Similarly, the vector angular
momentum is zero, since
![]() .
.
For
![]() , the result is
, the result is
![\begin{displaymath}
\mathbf{I}\eqsp
\begin{array}{r}\left[\begin{array}{ccc} 1 ...
...egin{array}{c} 1 \\ [2pt] 0 \\ [2pt] 0\end{array}\right]m = m,
\end{displaymath}](http://www.dsprelated.com/josimages_new/pasp/img2902.png)
Off-Diagonal Terms in Moment of Inertia Tensor
This all makes sense, but what about those ![]() off-diagonal terms in
off-diagonal terms in
![]() ? Consider the vector angular momentum (§B.4.14):
? Consider the vector angular momentum (§B.4.14):
![$\displaystyle \underline{L}\eqsp \mathbf{I}\,\underline{\omega}\eqsp
m\left[\b...
...begin{array}{c} \omega_1 \\ [2pt] \omega_2 \\ [2pt] \omega_3\end{array}\right]
$](http://www.dsprelated.com/josimages_new/pasp/img2907.png)
Principal Axes of Rotation
A principal axis of rotation (or principal direction) is
an eigenvector of the mass moment of inertia tensor (introduced
in the previous section) defined relative to some point (typically the
center of mass). The corresponding eigenvalues are called the
principal moments of inertia.
Because the moment of inertia tensor is defined relative to the point
![]() in the space, the principal axes all pass through that point
(usually the center of mass).
in the space, the principal axes all pass through that point
(usually the center of mass).
As derived above (§B.4.14), the angular momentum vector is given by the moment of inertia tensor times the angular-velocity vector:
Positive Definiteness of the Moment of Inertia Tensor
From the form of the moment of inertia tensor introduced in Eq.![]() (B.24)
(B.24)
![\begin{eqnarray*}
I &=& \underline{\tilde{\omega}}^T\mathbf{I}\,\underline{\tild...
...\cal P}_{\underline{x}}(\underline{\tilde{\omega}})\right] \ge 0
\end{eqnarray*}](http://www.dsprelated.com/josimages_new/pasp/img2916.png)
since
![]() is unit length, and projecting it onto any other vector
can only shorten it or leave it unchanged. That is,
is unit length, and projecting it onto any other vector
can only shorten it or leave it unchanged. That is,
![]() , with equality occurring for
, with equality occurring for
![]() for any nonzero
for any nonzero
![]() . Zooming out,
of course we expect any moment of inertia
. Zooming out,
of course we expect any moment of inertia ![]() for a positive
mass
for a positive
mass ![]() to be nonnegative. Thus,
to be nonnegative. Thus,
![]() is symmetric
nonnegative definite. If furthermore
is symmetric
nonnegative definite. If furthermore
![]() and
and
![]() are not
collinear, i.e., if there is any nonzero angle between them, then
are not
collinear, i.e., if there is any nonzero angle between them, then
![]() is positive definite (and
is positive definite (and ![]() ). As is well known in
linear algebra [329], real, symmetric, positive-definite
matrices have orthogonal eigenvectors and real, positive
eigenvalues. In this context, the orthogonal eigenvectors are
called the principal axes of rotation. Each corresponding
eigenvalue is the moment of inertia about that principal axis--the
corresponding principal moment of inertia. When angular velocity
vectors
). As is well known in
linear algebra [329], real, symmetric, positive-definite
matrices have orthogonal eigenvectors and real, positive
eigenvalues. In this context, the orthogonal eigenvectors are
called the principal axes of rotation. Each corresponding
eigenvalue is the moment of inertia about that principal axis--the
corresponding principal moment of inertia. When angular velocity
vectors
![]() are expressed as a linear combination of the principal
axes, there are no cross-terms in the moment of inertia tensor--no
so-called products of inertia.
are expressed as a linear combination of the principal
axes, there are no cross-terms in the moment of inertia tensor--no
so-called products of inertia.
The three principal axes are unique when the eigenvalues of
![]() (principal moments of inertia) are distinct. They are
not unique when there are repeated eigenvalues, as in the example
above of a disk rotating about any of its diameters
(§B.4.4). In that example, one principal
axis, the one corresponding to eigenvalue
(principal moments of inertia) are distinct. They are
not unique when there are repeated eigenvalues, as in the example
above of a disk rotating about any of its diameters
(§B.4.4). In that example, one principal
axis, the one corresponding to eigenvalue ![]() , was
, was
![]() (i.e.,
orthogonal to the disk and passing through its center), while any two
orthogonal diameters in the plane of the disk may be chosen as the
other two principal axes (corresponding to the repeated eigenvalue
(i.e.,
orthogonal to the disk and passing through its center), while any two
orthogonal diameters in the plane of the disk may be chosen as the
other two principal axes (corresponding to the repeated eigenvalue
![]() ).
).
Symmetry of the rigid body about any axis
![]() (passing through the
origin) means that
(passing through the
origin) means that
![]() is a principal direction. Such a symmetric
body may be constructed, for example, as a solid of
revolution.B.26In rotational dynamics, this case is known as the symmetric top
[270]. Note that the center of mass will lie
somewhere along an axis of symmetry. The other two principal axes can
be arbitrarily chosen as a mutually orthogonal pair in the (circular)
plane orthogonal to the
is a principal direction. Such a symmetric
body may be constructed, for example, as a solid of
revolution.B.26In rotational dynamics, this case is known as the symmetric top
[270]. Note that the center of mass will lie
somewhere along an axis of symmetry. The other two principal axes can
be arbitrarily chosen as a mutually orthogonal pair in the (circular)
plane orthogonal to the
![]() axis, intersecting at the
axis, intersecting at the
![]() axis. Because of the circular symmetry about
axis. Because of the circular symmetry about
![]() , the two
principal moments of inertia in that plane are equal. Thus the moment
of inertia tensor can be diagonalized to look like
, the two
principal moments of inertia in that plane are equal. Thus the moment
of inertia tensor can be diagonalized to look like
![$\displaystyle \mathbf{I}= \left[\begin{array}{ccc}
I_1 & 0 & 0\\ [2pt]
0 & I_2 & 0\\ [2pt]
0 & 0 & I_2
\end{array}\right],
$](http://www.dsprelated.com/josimages_new/pasp/img2925.png)
Rotational Kinetic Energy Revisited
If a point-mass is located at
![]() and is rotating about an
axis-of-rotation
and is rotating about an
axis-of-rotation
![]() with angular velocity
with angular velocity ![]() , then the
distance from the rotation axis to the mass is
, then the
distance from the rotation axis to the mass is
![]() ,
or, in terms of the vector cross product,
,
or, in terms of the vector cross product,
![]() . The tangential velocity of the mass is
then
. The tangential velocity of the mass is
then ![]() , so that the kinetic energy can be expressed as
(cf. Eq.
, so that the kinetic energy can be expressed as
(cf. Eq.![]() (B.23))
(B.23))
where
In a collection of ![]() masses
masses ![]() having velocities
having velocities
![]() , we of
course sum the individual kinetic energies to get the total kinetic
energy.
, we of
course sum the individual kinetic energies to get the total kinetic
energy.
Finally, we may also write the rotational kinetic energy as half the inner product of the angular-velocity vector and the angular-momentum vector:B.27
Torque
![\includegraphics[width=1.1in]{eps/torque}](http://www.dsprelated.com/josimages_new/pasp/img2937.png) |
When twisting things, the rotational force we apply about the center
is called a torque (or moment, or moment of
force). Informally, we think of the torque as the tangential
applied force ![]() times the moment arm (length of the
lever arm)
times the moment arm (length of the
lever arm) ![]()
as depicted in Fig.B.7. The moment arm is the distance from the applied force to the point being twisted. For example, in the case of a wrench turning a bolt,
For more general applied forces
![]() , we may compute the
tangential component
, we may compute the
tangential component
![]() by projecting
by projecting
![]() onto the
tangent direction. More precisely, the torque
onto the
tangent direction. More precisely, the torque ![]() about the
origin
about the
origin
![]() applied at a point
applied at a point
![]() may be defined by
may be defined by
where
Note that the torque vector
![]() is orthogonal to both the lever
arm and the tangential-force direction. It thus points in the
direction of the angular velocity vector (along the axis of rotation).
is orthogonal to both the lever
arm and the tangential-force direction. It thus points in the
direction of the angular velocity vector (along the axis of rotation).
The torque magnitude is
Newton's Second Law for Rotations
The rotational version of Newton's law ![]() is
is
where
![\begin{eqnarray*}
\tau &=& \dot{L} \,\eqss \, I\dot{\omega}\,\isdefss \, I\alpha\\ [5pt]
f &=& \dot{p} \,\eqss \, m\dot{v}\,\isdefss \, ma
\end{eqnarray*}](http://www.dsprelated.com/josimages_new/pasp/img2949.png)
To show that Eq.![]() (B.28) results from Newton's second law
(B.28) results from Newton's second law ![]() ,
consider again a mass
,
consider again a mass ![]() rotating at a distance
rotating at a distance ![]() from an axis
of rotation, as in §B.4.3 above, and
let
from an axis
of rotation, as in §B.4.3 above, and
let ![]() denote a tangential force on the mass, and
denote a tangential force on the mass, and ![]() the corresponding tangential acceleration. Then we have, by Newton's
second law,
the corresponding tangential acceleration. Then we have, by Newton's
second law,
In summary, force equals the time-derivative of linear momentum, and torque equals the time-derivative of angular momentum. By Newton's laws, the time-derivative of linear momentum is mass times acceleration, and the time-derivative of angular momentum is the mass moment of inertia times angular acceleration:
Equations of Motion for Rigid Bodies
We are now ready to write down the general equations of motion for
rigid bodies in terms of ![]() for the center of mass and
for the center of mass and
![]() for the rotation of the body about its center of mass.
for the rotation of the body about its center of mass.
As discussed above, it is useful to decompose the motion of a rigid body into
- (1)
- the linear velocity
 of its center of mass, and
of its center of mass, and
- (2)
- its angular velocity
 about its center of mass.
about its center of mass.
The linear motion is governed by Newton's second law
![]() , where
, where ![]() is the total mass,
is the total mass,
![]() is the
velocity of the center-of-mass, and
is the
velocity of the center-of-mass, and
![]() is the sum of all external
forces on the rigid body. (Equivalently,
is the sum of all external
forces on the rigid body. (Equivalently,
![]() is the sum of the
radial force components pointing toward or away from the center of
mass.) Since this is so straightforward, essentially no harder than
dealing with a point mass, we will not consider it further.
is the sum of the
radial force components pointing toward or away from the center of
mass.) Since this is so straightforward, essentially no harder than
dealing with a point mass, we will not consider it further.
The angular motion is governed the rotational version of Newton's second law introduced in §B.4.19:
where
The driving torque
![]() is given by the resultant moment of
the external forces, using Eq.
is given by the resultant moment of
the external forces, using Eq.![]() (B.27) for each external force to
obtain its contribution to the total moment. In other words, the
external moments (tangential forces times moment arms) sum up for the
net torque just like the radial force components summed to produce the
net driving force on the center of mass.
(B.27) for each external force to
obtain its contribution to the total moment. In other words, the
external moments (tangential forces times moment arms) sum up for the
net torque just like the radial force components summed to produce the
net driving force on the center of mass.
Body-Fixed and Space-Fixed Frames of Reference
Rotation is always about some (instantaneous) axis of rotation that is
free to change over time. It is convenient to express rotations in a
coordinate system having its origin (
![]() ) located at the
center-of-mass of the rigid body (§B.4.1), and its coordinate axes
aligned along the principal directions for the body (§B.4.16).
This body-fixed frame then moves within a stationary
space-fixed frame (or ``star frame'').
) located at the
center-of-mass of the rigid body (§B.4.1), and its coordinate axes
aligned along the principal directions for the body (§B.4.16).
This body-fixed frame then moves within a stationary
space-fixed frame (or ``star frame'').
In Eq.![]() (B.29) above, we wrote down Newton's second law for angular
motion in the body-fixed frame, i.e., the coordinate system
having its origin at the center of mass. Furthermore, it is simplest
(
(B.29) above, we wrote down Newton's second law for angular
motion in the body-fixed frame, i.e., the coordinate system
having its origin at the center of mass. Furthermore, it is simplest
(
![]() is diagonal) when its axes lie along principal directions
(§B.4.16).
is diagonal) when its axes lie along principal directions
(§B.4.16).
As an example of a local body-fixed coordinate system, consider a spinning top. In the body-fixed frame, the ``vertical'' axis coincides with the top's axis of rotation (spin). As the top loses rotational kinetic energy due to friction, the top's rotation-axis precesses around a circle, as observed in the space-fixed frame. The other two body-fixed axes can be chosen as any two mutually orthogonal axes intersecting each other (and the spin axis) at the center of mass, and lying in the plane orthogonal to the spin axis. The space-fixed frame is of course that of the outside observer's inertial frameB.28in which the top is spinning.
Angular Motion in the Space-Fixed Frame
Let's now consider angular motion in the presence of linear motion of the center of mass. In general, we have [270]
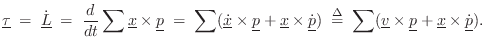
Euler's Equations for Rotations in the Body-Fixed Frame
Suppose now that the body-fixed frame is rotating in the space-fixed
frame with angular velocity
![]() . Then the total torque on the rigid
body becomes [270]
. Then the total torque on the rigid
body becomes [270]
Similarly, the total external forces on the center of mass become
![$\displaystyle \underline{L}\eqsp \left[\begin{array}{c} I_1\omega_1 \\ [2pt] I_2\omega_2 \\ [2pt] I_3\omega_3\end{array}\right]
$](http://www.dsprelated.com/josimages_new/pasp/img2969.png)
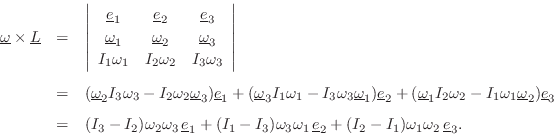
Substituting this result into Eq.![]() (B.30), we obtain the following
equations of angular motion for an object rotating in the body-fixed
frame defined by its three principal axes of rotation:
(B.30), we obtain the following
equations of angular motion for an object rotating in the body-fixed
frame defined by its three principal axes of rotation:
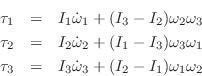
These are call Euler's
equations:B.29Since these equations are in the body-fixed frame, ![]() is the mass
moment of inertia about principal axis
is the mass
moment of inertia about principal axis ![]() , and
, and ![]() is the
angular velocity about principal axis
is the
angular velocity about principal axis ![]() .
.
Examples
For a uniform sphere, the cross-terms disappear and the moments of
inertia are all the same, leaving
![]() , for
, for ![]() .
Since any three orthogonal vectors can serve as eigenvectors of the
moment of inertia tensor, we have that, for a uniform sphere, any
three orthogonal axes can be chosen as principal axes.
.
Since any three orthogonal vectors can serve as eigenvectors of the
moment of inertia tensor, we have that, for a uniform sphere, any
three orthogonal axes can be chosen as principal axes.
For a cylinder that is not spinning about its axis, we similarly
obtain two uncoupled equations
![]() , for
, for ![]() , given
, given
![]() (no spin). Note, however, that if we replace the
circular cross-section of the cylinder by an ellipse, then
(no spin). Note, however, that if we replace the
circular cross-section of the cylinder by an ellipse, then
![]() and there is a coupling term that drives
and there is a coupling term that drives
![]() (unless
(unless ![]() happens to cancel it).
happens to cancel it).
Next Section:
Properties of Elastic Solids
Previous Section:
Momentum








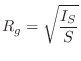
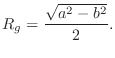
![\includegraphics[width=1.5in]{eps/massrodmass}](http://www.dsprelated.com/josimages_new/pasp/img2758.png)
![$\displaystyle \left\vert \begin{array}{ccc}
\underline{e}_1 & \underline{e}_2 &...
...ine{e}_3\\ [2pt]
x_1 & x_2 & x_3\\ [2pt]
y_1 & y_2 & y_3
\end{array}\right\vert$](http://www.dsprelated.com/josimages_new/pasp/img2809.png)
![$\displaystyle \left[\begin{array}{ccc}
0 & -x_3 & x_2\\ [2pt]
x_3 & 0 & -x_1\\ ...
...}\right]
\left[\begin{array}{c} x_1 \\ [2pt] x_2 \\ [2pt] x_3\end{array}\right]$](http://www.dsprelated.com/josimages_new/pasp/img2811.png)